题目内容
一次函数 的图像与反比例函数
的图像与反比例函数 的图象交于A(-2,1),B(1,n)两点.
的图象交于A(-2,1),B(1,n)两点.
(1)试确定上述反比例函数和一次函数的表达式;
(2)求△OAB的面积.
(3)写出反比例函数值大于一次函数值的自变量x的取值范围.
(1)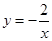 ,
,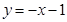 ;(2)1.5;(3)
;(2)1.5;(3) 或
或 .
.
解析试题分析:(1)先把A点坐标代入 ,便可求出m的值,进而求出反比例函数的解析式,再把B点代入函数解析式便可求出B点的坐标,再用待定系数法便可求出一次函数的解析式;
,便可求出m的值,进而求出反比例函数的解析式,再把B点代入函数解析式便可求出B点的坐标,再用待定系数法便可求出一次函数的解析式;
(2)由(1)求出直线与x轴的交点坐标,将△ABO的面积分成两个三角形的面积来求即可;
(3)由一次函数与反比例函数的图象便可直接解答.
试题解析:(1)把A(﹣2,1)代入 ;得
;得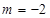 ;∴反比例函数为
;∴反比例函数为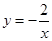 ;把B(1,n)代入
;把B(1,n)代入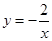 得:
得: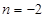 ;∴点B坐标为(1,﹣2),把A(﹣2,1),B(1,﹣2)代入一次函数
;∴点B坐标为(1,﹣2),把A(﹣2,1),B(1,﹣2)代入一次函数 得,解得
得,解得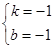 ,∴一次函数的解析式为
,∴一次函数的解析式为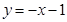 ;
;
(2)令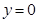 得:
得: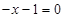 ,即
,即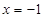 ,∴S△ABO=
,∴S△ABO=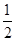 ×1×2+
×1×2+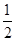 ×1×1=1.5.
×1×1=1.5.
(3)由函数图象可知,反比例函数的值大于一次函数的值时x的取值范围为 或
或 .
.
考点:1.反比例函数与一次函数的交点问题;2.反比例函数系数k的几何意义;3.三角形的面积.

练习册系列答案
相关题目
某公司从2009年开始投入技术改造资金,经技术改进后,其产品的生产成本不断降低,具体数据如表:
| 年度 | 2009 | 2010 | 2011 | 2012 |
| 投入技改资金x(万元) | 2.5 | 3 | 4 | 4.5 |
| 产品成本y(万元/件) | 7.2 | 6 | 4.5 | 4 |
(2)按照上述函数模型,若2013年已投入技改资金5万元
①预计生产成本每件比2012年降低多少元?
②如果打算在2013年把每件产品的成本降低到3.2万元,则还需投入技改资金多少万元?
 上,且
上,且 ,;分别过点A、B向x轴、y轴作垂线段,垂足分别为C、D、E、F,AC与BF相交于G点,四边形FOCG的面积为2,五边形AEODB的面积为14,那么双曲线的解析为 .
,;分别过点A、B向x轴、y轴作垂线段,垂足分别为C、D、E、F,AC与BF相交于G点,四边形FOCG的面积为2,五边形AEODB的面积为14,那么双曲线的解析为 .
 (k>0)与矩形两边AB、BC分别交于E、F.
(k>0)与矩形两边AB、BC分别交于E、F.
 在第一象限内的交点.
在第一象限内的交点. 的坐标及
的坐标及 的值;
的值; 轴上确定一点
轴上确定一点 ,使
,使 ,求出点
,求出点
 (m为常数)的图象与反比例函数
(m为常数)的图象与反比例函数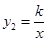 (k为常数,
(k为常数,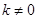 )的图象相交于点 A(1,3).
)的图象相交于点 A(1,3).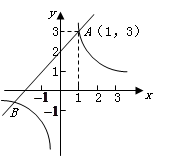
 的坐标;
的坐标;  的自变量
的自变量 的取值范围.
的取值范围.
 个单位后,使点B恰好落在双曲线上,求
个单位后,使点B恰好落在双曲线上,求 的图象经过点C,一次函数
的图象经过点C,一次函数 的图象经过点C,一次函数
的图象经过点C,一次函数