题目内容
【题目】已知有公共顶点![]() 的△
的△![]() 和△
和△![]() 都是等边三角形,且
都是等边三角形,且![]() >
>![]() .
.

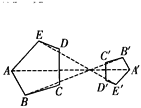
(1)如图1,当点![]() 恰好在
恰好在![]() 的延长线上时,连结
的延长线上时,连结![]() ,
,![]() 分别交
分别交![]() ,
,![]() 于点
于点![]() ,
,![]() .
.
①求证:![]() ;
;
②连接![]() ,求证:
,求证:![]() ∥
∥![]() ;
;
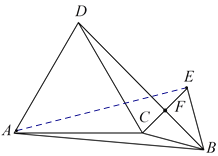
(2)图2是由图1中的△![]() 绕点
绕点![]() 顺时针旋转角
顺时针旋转角![]() (
(![]() <
<![]() <
<![]() )得到,使得
)得到,使得![]() 恰好经过
恰好经过![]() 的中点
的中点![]() ,试猜想线段
,试猜想线段![]() ,
,![]() ,
,![]() 之间的数量关系,并说明理由.
之间的数量关系,并说明理由.
【答案】(1)①证明见解析;②证明见解析;(2)猜想:BC2+BD2=AB2,理由见解析.
【解析】
(1)①先由等边三角形得出CA=CD,CB=CE,∠ACD=∠BCE =60°,从而判断出∠ACE=∠DCB,得到△ACE≌△DCB,根据全等三角形的对应边相等即可得证;
②由∠ACD=∠BCE =60°可得∠MCN =60°,由△ACE≌△DCB可得∠CAE=∠CDB,然后根据ASA证明△ACM≌△DCN,从而得CM=CN,继而得到△MCN是等边三角形,进而根据平行线的判定即可得证;
(2)猜想:BC2+BD2=AB2,理由为:如图,连接AE,仿照(1)①证明△ACE≌△DCB,从而可得 AE=BD,∠AEC=∠DBC,再根据等边三角形的性质可得∠CBF=30°,继而可得∠AEB=∠AEC+∠BEC=90°,利用勾股定理可得AE2+BE2=AB2,等量代换即可得BC2+BD2=AB2.
(1)①∵△ACD,△BCE都是等边三角形,
∴∠DCA=∠BCE=60°,CA=CD,CB=CE,
∵∠ACE=∠ACD+∠MCN,∠DCB=∠MCN+∠BCE,
∴∠ACE=∠DCB,
∴△ACE≌△DCB(SAS),
∴AE=BD;
②∵A、C、B共线,∠ACD=∠BCE =60°,
∴∠MCN=180°-∠ACD-∠BCE=60°,
∴∠ACM=∠DCN,
∵△ACE≌△DCB,
∴∠CAM=∠CDN,
又∵CA=CD,
∴△ACM≌△DCN,
∴CM=CN,
又∵∠MCN=60°,
∴△MCN是等边三角形,
∴∠MNC=60°,
又∵∠BCE=60°,
∴∠MNC=∠BCE,
∴MN//AB;
(2)猜想:BC2+BD2=AB2,理由如下:
如图,连接AE,
∵△ACD,△BCE都是等边三角形,
∴∠DCA=∠BCE=∠BEC=∠CBE=60°,CA=CD,CB=CE=BE,
∵∠ACE=∠ACD+∠MCN,∠DCB=∠MCN+∠BCE,
∴∠ACE=∠DCB,
∴△ACE≌△DCB(SAS),
∴AE=BD,∠AEC=∠DBC,
又∵F为BC中点,
∴∠CBF=![]() ∠CBE=30°,
∠CBE=30°,
∴∠AEC=30°,
∴∠AEB=∠AEC+∠BEC=90°,
∴AE2+BE2=AB2,
∴BC2+BD2=AB2.

 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案