题目内容
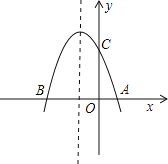
【题目】如图,抛物线y=﹣x2+bx+c与x轴交于A(1,0),B(﹣3,0)两点.
(1)求该抛物线的解析式;
(2)设(1)中的抛物线交y轴与C点,在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由;
(3)在(1)中的抛物线上的第二象限上是否存在一点P,使△PBC的面积最大?若存在,求出点P的坐标及△PBC的面积最大值;若没有,请说明理由.
【答案】(1)、y=-![]() -2x+3;(2)、Q(-1,2);(3)、(
-2x+3;(2)、Q(-1,2);(3)、(![]() ,
,![]() )
)
【解析】
试题分析:(1)、将点A和点B代入函数解析式,利用待定系数法求出函数解析式;(2)、根据题意得出A、B两点关于对称轴对称,则直线BC与x=-1的交点就是点Q,根据题意得出点C的坐标,然后利用待定系数法求出直线BC的解析式,从而得出点Q的坐标;(3)、首先设点P的坐标,然后根据△BPC的面积等于四边形BPCO的面积减去△BOC的面积,然后列出关于x的函数解析式,从而得出最大值.
试题解析:(1)、将A(1,0),B(﹣3,0)代y=﹣x2+bx+c中得
![]() ∴
∴![]() ∴抛物线解析式为:y=﹣x2﹣2x+3;
∴抛物线解析式为:y=﹣x2﹣2x+3;
(2)、存在
理由如下:由题知A、B两点关于抛物线的对称轴x=﹣1对称
∴直线BC与x=﹣1的交点即为Q点,此时△AQC周长最小∵y=﹣x2﹣2x+3 ∴C的坐标为:(0,3)
直线BC解析式为:y=x+3 Q点坐标即为![]() 解得
解得![]() ∴Q(﹣1,2);
∴Q(﹣1,2);
(3)、存在.
理由如下:设P点(x,﹣x2﹣2x+3)(﹣3<x<0) ∵S△BPC=S四边形BPCO﹣S△BOC=S四边形BPCO﹣![]()
若S四边形BPCO有最大值,则S△BPC就最大,
∴S四边形BPCO=S△BPE+S直角梯形PEOC=![]() BEPE+
BEPE+![]() OE(PE+OC)=
OE(PE+OC)=![]() (x+3)(﹣x2﹣2x+3)+
(x+3)(﹣x2﹣2x+3)+![]() (﹣x)(﹣x2﹣2x+3+3)
(﹣x)(﹣x2﹣2x+3+3)
=![]()
当x=﹣![]() 时,S四边形BPCO最大值=
时,S四边形BPCO最大值=![]() ∴S△BPC最大=
∴S△BPC最大=![]()
当x=﹣![]() 时,﹣x2﹣2x+3=
时,﹣x2﹣2x+3=![]() ∴点P坐标为(﹣
∴点P坐标为(﹣![]() ,
,![]() ).
).
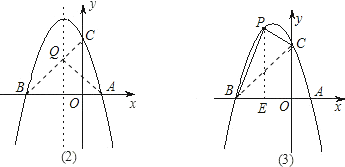

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案