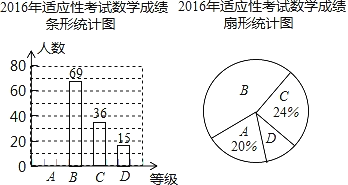
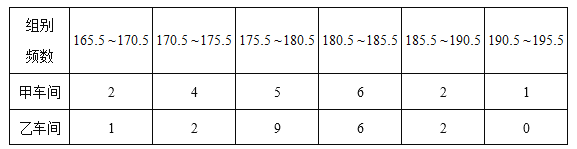
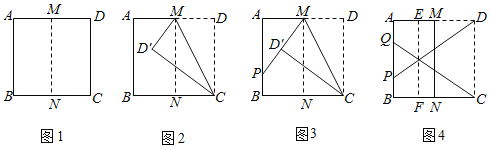
题目内容
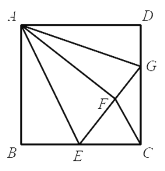
【题目】如果一个圆上所有的点都在一个角的内部或边上,那么称这个圆为该角的角内圆.特别地,当这个圆与角的至少一边相切时,称这个圆为该角的角内相切圆.在平面直角坐标系xOy中,点E,F分别在x轴的正半轴和y轴的正半轴上.
⑴ 分别以点![]() (1,0),
(1,0),![]() (1,1),
(1,1),![]() (3,2)为圆心,1为半径作圆,得到⊙
(3,2)为圆心,1为半径作圆,得到⊙![]() ,⊙
,⊙![]() 和⊙
和⊙![]() ,其中是
,其中是![]() 的角内圆的是 ;
的角内圆的是 ;
⑵ 如果以点![]() (
(![]() ,2)为圆心,以1为半径的⊙
,2)为圆心,以1为半径的⊙![]() 为
为![]() 的角内圆,且与一次函数图像
的角内圆,且与一次函数图像![]() 有公共点,求
有公共点,求![]() 的取值范围;
的取值范围;
⑶ 点![]() 在第一象限内,如果存在一个半径为1且过点
在第一象限内,如果存在一个半径为1且过点![]() (2,
(2,![]() )的圆为
)的圆为![]() 的角内相切圆,直接写出
的角内相切圆,直接写出![]() 的取值范围.
的取值范围.
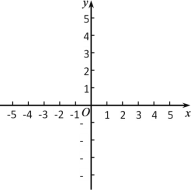
【答案】(1) ⊙B,⊙C;(2) ![]() ;(3) 60°≤∠EOM<90°.
;(3) 60°≤∠EOM<90°.
【解析】
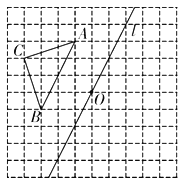
(1)画出图象,根据角内相切圆的定义判断即可.
(2)求出两种特殊位置时t的值即可判断.
(3)如图3中,连接OP,OM.首先求出∠POE,根据图象可知当射线OM在∠POF的内部(包括射线OP,不包括射线OF)时,存在一个半径为1且过点![]() 的圆为∠EOM的角内相切圆.
的圆为∠EOM的角内相切圆.
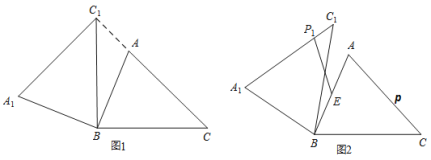
⑴ 如图1中,![]() 点
点![]() (1,0),
(1,0),![]() (1,1),
(1,1),![]() (3,2)
(3,2)
![]() 观察图象可知,⊙B和⊙C是∠EOF的角内圆.
观察图象可知,⊙B和⊙C是∠EOF的角内圆.
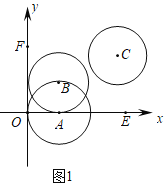
故答案为:⊙B,⊙C;
⑵ 如图,当⊙![]() 与
与![]() 轴相切时,设切点为
轴相切时,设切点为![]() ,则
,则![]() ,可得
,可得![]() .
.
当⊙![]() 与
与![]() 相切时,设切点为
相切时,设切点为![]() ,连接
,连接![]() ,设直线
,设直线![]() 与直线
与直线![]() 交于点
交于点![]() ,
,
由![]() 的性质得:
的性质得:![]()
![]()
则△![]() ,△
,△![]() 都是等腰直角三角形,
都是等腰直角三角形,
![]()
![]() ,
,
∴![]() ,
,![]() ,
,
∴![]()
可得![]() ,
,
可知,满足条件的![]() 的取值范围是
的取值范围是![]() .
.
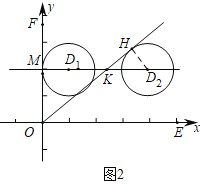
⑶如图3中,连接OP,OM.
∵![]() ,
,
∴![]()
∴∠POE=60°,
观察图象可知当射线OM在∠POF的内部(包括射线OP,不包括射线OF)时,
存在一个半径为1且过点![]() 的圆为∠EOM的角内相切圆,
的圆为∠EOM的角内相切圆,
∴ 60°≤∠EOM<90°.


 综合自测系列答案
综合自测系列答案【题目】车间有20名工人,某天他们生产的零件个数统计如下表.
车间20名工人某一天生产的零件个数统计表
生产零件的个数(个) | 9 | 10 | 11 | 12 | 13 | 15 | 16 | 19 | 20 |
工人人数(人) | 1 | 1 | 6 | 4 | 2 | 2 | 2 | 1 | 1 |
(1)求这一天20名工人生产零件的平均个数;
(2)为了提高大多数工人的积极性,管理者准备实行“每天定额生产,超产有奖”的措施.如果你是管理者,从平均数、中位数、众数的角度进行分析,你将如何确定这个“定额”?