题目内容
【题目】如图,已知OABC是一张放在平面直角坐标系中的矩形纸片,O为坐标原点,点A(15,0),点C(0,9),在边AB上任取一点D,将△AOD沿OD翻折,使点A落在BC边上,记为点E.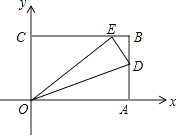
(1)OA的长= , OE的长= , CE的长= , AD的长=;
(2)设点P在x轴上,且OP=EP,求点P的坐标.
【答案】
(1)15,15,12,5
(2)解:过点E作EF⊥OA于点F,
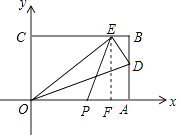
∵∠COA=∠BCO=∠OFE=90°,
∴四边形OCEF是矩形,
∴OF=CE=12,EF=OC=9,
设OP=m,则EP=OP=m,PF=12﹣m,
在Rt△EPF中,PF2+EF2=EP2,
∴(12﹣m)2+92=m2,
解得:m= ![]() ,
,
∴点P的坐标为:( ![]() ,0).
,0).
【解析】解:(1)∵OABC是一张放在平面直角坐标系中的矩形纸片,O为坐标原点,点A(15,0),点C(0,9),
∴OA=BC=15,OC=AB=9,
∵将△AOD沿OD翻折,使点A落在BC边上,记为点E,
∴OE=OA=15,
∴CE= ![]() =12,
=12,
∴BE=BC﹣CE=3,
设AD=x,则DE=AD=x,BD=AB﹣AD=9﹣x,
∵BD2+BE2=DE2,
∴(9﹣x)2+32=x2,
解得:x=5,
∴AD=5.
所以答案是:15,15,12,5;
【考点精析】本题主要考查了矩形的性质和轴对称图形的相关知识点,需要掌握矩形的四个角都是直角,矩形的对角线相等;两个完全一样的图形关于某条直线对折,如果两边能够完全重合,我们就说这两个图形成轴对称,这条直线就对称轴才能正确解答此题.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目