题目内容
【题目】如图,在ABCD中,BC=2AB=4,点E、F分别是BC、AD的中点.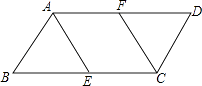
(1)求证:△ABE≌△CDF;
(2)当四边形AECF为菱形时,求出该菱形的面积.
【答案】
(1)证明:∵在ABCD中,AB=CD,
∴BC=AD,∠ABC=∠CDA.
又∵BE=EC= ![]() BC,AF=DF=
BC,AF=DF= ![]() AD,
AD,
∴BE=DF.
∴△ABE≌△CDF.
(2)解:∵四边形AECF为菱形,
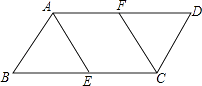
∴AE=EC.
又∵点E是边BC的中点,
∴BE=EC,即BE=AE.
又BC=2AB=4,
∴AB= ![]() BC=BE,
BC=BE,
∴AB=BE=AE,即△ABE为等边三角形,
ABCD的BC边上的高为2×sin60°= ![]() ,
,
∴菱形AECF的面积为2 ![]() .
.
【解析】(1)在ABCD中,AB=CD,得到BC=AD,∠ABC=∠CDA,又因为BE=EC= BC÷2,AF=DF= AD÷2,得到BE=DF,得到△ABE≌△CDF;(2)由四边形AECF为菱形,得到AE=EC,得到AE=EC,又点E是边BC的中点,得到BE=EC,即BE=AE,又BC=2AB=4,得到AB=BE,得到AB=BE=AE,即△ABE为等边三角形,所以ABCD的BC边上的高为2×sin60°=![]() ,菱形AECF的面积为2
,菱形AECF的面积为2![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目