��Ŀ����
����Ŀ�����壺���������У���һ�ߵ��е㵽�����ߵĸ��ߵľ�����������ߵ��д��࣮
������ͼ�٣�����ABC�У�DΪ��BC���е㣬AE��BC��E�����߶�DE�ij�������BC���д��࣮
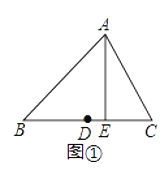
��1����������һ�ߵ��д���Ϊd��d��0������d=0����������������һ����________���ƶϵ���ѧ������________��
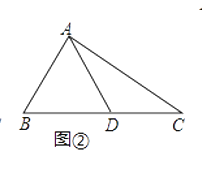
��2����ͼ�ڣ�����ABC�У���B=45����AB=![]() ��BC=8��ADΪ��BC�����ߣ����BC���д��࣮
��BC=8��ADΪ��BC�����ߣ����BC���д��࣮
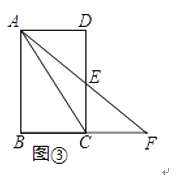
��3����ͼ�ۣ��ھ���ABCD�У�AB=6��AD=4����EΪ��CD���е㣬����AE���ӳ���BC���ӳ����ڵ�F������AC������ACF�б�AF���д��࣮
���𰸡���1�����������Σ��߶εĴ�ֱƽ�����ϵĵ㵽���˵ľ�����ȣ���2��1����3��![]() .
.
�������������������1�������߶εĴ�ֱƽ���ߵ����ʼ����жϡ�
��2����ͼ���У���AE��BC��E��������֪�ó�AE=BE�������BD�ij����������DE�ij���
��3����ͼ���У���CH��AF��H����֤��ADE�ա�FCE���ó�AE=EF�����ù��ɶ������AE�ij���Ȼ��֤����ADE�ס�CHE�������������EH���ɡ�
�⣺��1�����������Σ��߶εĴ�ֱƽ�����ϵĵ㵽���˵ľ������
��2���⣺��ͼ���У���AE��BC��E��
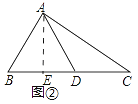
��Rt��ABE�У��ߡ�AEB=90�㣬��B=45�㣬AB=3 ![]() ��
��
��AE=BE=3��
��ADΪBC�����ߣ�BC=8��
��BD=DC=4��
��DE=BD��BE=4��3=1��
���BC���д���Ϊ1
��3���⣺��ͼ���У���CH��AF��H��
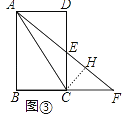
���ı���ABCD�Ǿ��Σ�
���D=��EHC=��ECF=90�㣬AD��BF��
��DE=EC����AED=��CEF��
���ADE�ա�FCE��
��AE=EF��
��Rt��ADE����AD=4��DE=3��
��AE= ![]() =5��
=5��
�ߡ�D=EHC����AED=��CEH��
���ADE�ס�CHE��
�� ![]() =
= ![]() ��
��
�� ![]() =
= ![]() ��
��
��EH= ![]() ��
��
���ACF�б�AF���д���Ϊ ![]()