题目内容
【题目】已知抛物线y=ax2﹣2anx+an2+n+3的顶点P在一条定直线l上.
(1)直接写出直线l的解析式;
(2)对于任意非零实数a,存在确定的n的值,使抛物线与x轴有唯一的公共点,求此时n的值;
(3)当点P在x轴上时,抛物线与直线l的另一个交点Q,过点Q作x轴的平行线,交抛物线于点A,过点Q作y轴的平行线,交x轴于点B,求![]() 的值或取值范围.
的值或取值范围.
【答案】(1)y=x+3;(2)﹣3;(3)2
【解析】
(1)先把抛物线解析式化成顶点式,确定出顶点坐标,即可得出结论;
(2)令抛物线中的y=0用一元二次方程根的判别式即可得出结论;
(3)先确定出n的值,进而得出点Q的坐标,即可确定出点A,B坐标,最后确定出AQ,BQ,即可得到结论.
(1)∵抛物线y=ax2﹣2anx+an2+n+3=a(x﹣n)2+(n+3),∴抛物线P(n,n+3).
∵顶点P在一条定直线l上,令n=x,n+3=y,∴y=x+3,即:直线l的解析式为y=x+3;
(2)抛物线与x轴有唯一的公共点,令y=0,即:ax2﹣2anx+an2+n+3=0,∴△=(﹣2an)2﹣4a×(an2+n+3)=﹣4a(n+3)=0.
∵任意非零实数a,∴n+3=0,∴n=﹣3,∴抛物线与x轴有唯一的公共点,此时n的值为﹣3;
(3)由(1)知,P(n,n+3).
∵点P在x轴上,∴n+3=0,∴n=﹣3,∴抛物线y=a(x+3)2,①
∵直线l的解析式为y=x+3②,联立①②得Q(﹣3+![]() ).
).
∵过点Q作y轴的平行线,交x轴于点B,∴BQ=|![]() |.
|.
∵过点Q作x轴的平行线,交抛物线于点A,∴a(x+3)2=![]() ,∴x=﹣3±
,∴x=﹣3±![]() ,∴A(﹣3﹣
,∴A(﹣3﹣![]() ).
).
∵Q(﹣3+![]() ),∴AQ=|﹣3+
),∴AQ=|﹣3+![]() ﹣(﹣3﹣
﹣(﹣3﹣![]() )|=|
)|=|![]() |,∴
|,∴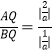 =2.
=2.

练习册系列答案
相关题目