题目内容
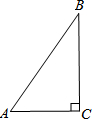如图，在△ABC中，∠C=90°，cosA=| 3 |
| 5 |
考点：解直角三角形
专题：
分析：先解直角三角形求出AB，再根据勾股定理求出BC的长，最后根据锐角三角函数的定义直接解答即可．
解答：解：∵在△ABC中，∠C=90°，cosA=
=
，AC=9，
∴AB=
=15，
根据勾股定理得：BC=12，
∴tanB=
=
=
．
| AC |
| AB |
| 3 |
| 5 |
∴AB=
| 9 | ||
|
根据勾股定理得：BC=12，
∴tanB=
| AC |
| BC |
| 9 |
| 12 |
| 3 |
| 4 |
点评：本题主要考查了余弦函数、正弦函数、正切函数的定义，是需要识记的内容．
练习册系列答案
阅读快车系列答案
相关题目
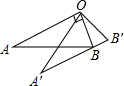如图，∠AOB=90°，将Rt△OAB绕点O按逆时针方向旋转至Rt△OA′B′，使点B恰好落在边A′B′上．已知tanA=
如图，为了估算河的宽度，小明采用的办法是：在河的对岸选取一点A，在近岸取点D，B，使得A，D，B在一条直线上，且与河的边沿垂直，测得BD=10m，然后又在垂直AB的直线上取点C，并量得BC=30m．如果DE=20m，则河宽AD为（ ）
已知AB=AD，∠BAD=∠CAE，请添加一个条件
如图，热气球的探测器显示，从热气球点A处看我市一栋高楼顶部B点处的仰角为60°，看这栋高楼底部C点处的俯角为30°，热气球与高楼的水平距离为66m，求这栋高楼的高度．（结果精确到0.1m，参考数据：
如图，△ABC中，点D、E分别在边AB、AC上，CD平分∠ACB，DE∥BC，若AC=10，AE=4，则BC=
我国南水北调中线工程的起点是某水库，按照工程计划，需对原水库大坝进行混凝土培厚加高，使坝高由原来的156米增加到173.2米，以抬高蓄水位．如图是某一段坝体加高工程的截面示意图，其中原坝体的高为BE，背水坡坡角∠BAE=69°，新坝体的高为DE，背水坡坡角∠DCE=60°．求工程完工后背水坡坡底端水平方向增加的宽度AC．（参考数据：sin69°≈0.93，cos69°≈0.36，tan69°≈2.60，