题目内容
【题目】如图,在△ABC中,AB=BC=4,AO=BO,P是射线CO上的一个动点,∠AOC=60°,则当△PAB为直角三角形时,AP的长为 .

【答案】![]() 或
或![]() 或2.
或2.
【解析】
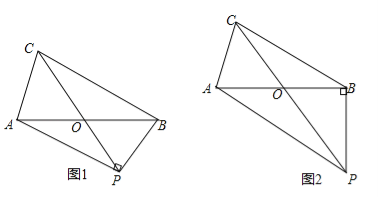
试题分析:当∠APB=90°时(如图1),∵AO=BO,∴PO=BO,∵∠AOC=60°,∴∠BOP=60°,∴△BOP为等边三角形,∵AB=BC=4,∴AP=ABsin60°=4×![]() =
=![]() ;
;
当∠ABP=90°时(如图2),∵∠AOC=∠BOP=60°,∴∠BPO=30°,∴BP=![]() =
=![]() =
=![]() ,在直角三角形ABP中,AP=
,在直角三角形ABP中,AP=![]() =
=![]() ;
;
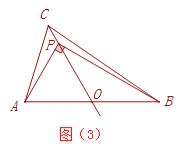
图(3)中,∠APB=90°,∵AO=BO,∠APB=90°,∴PO=AO=BO=2,又∠AOC=60°,∴△APO是等边三角形,∴AP=2;
故答案为:![]() 或
或![]() 或2.
或2.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目