题目内容
【题目】实验探究:
如图,![]() 和
和![]() 是有公共顶点的等腰直角三角形,
是有公共顶点的等腰直角三角形,![]() ,交于
,交于![]() 、
、![]() 点
点![]() .
.
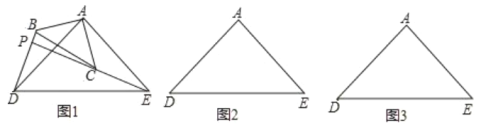
(问题发现)
(1)把![]() 绕点
绕点![]() 旋转到图
旋转到图![]() ,
,![]() 、
、![]() 的关系是_________(“相等”或“不相等”),请直接写出答案;
的关系是_________(“相等”或“不相等”),请直接写出答案;
(类比探究)
(2)若![]() ,
,![]() ,把
,把![]() 绕点
绕点![]() 旋转,当
旋转,当![]() 时,在图中作出旋转后的图形,并求出此时
时,在图中作出旋转后的图形,并求出此时![]() 的长;
的长;
(拓展延伸)
(3)在(2)的条件下,请直接写出旋转过程中线段![]() 的最小值为_________.
的最小值为_________.
【答案】(1)相等;(2)![]() 或
或![]() ;(3)1.
;(3)1.
【解析】
(1)依据△ABC和△ADE是有公共顶点的等腰直角三角形,∠BAC=∠DAE=90°,即可BA=CA,∠BAD=∠CAE,DA=EA,进而得到△ABD≌△ACE,可得出BD=CE;
(2)分两种情况:依据∠PDA=∠AEC,∠PCD=∠ACE,可得△PCD∽△ACE,即可得到![]() ,进而得到PD=
,进而得到PD=![]() ;依据∠ABD=∠PBE,∠BAD=∠BPE=90°,可得△BAD∽△BPE,即可得到
;依据∠ABD=∠PBE,∠BAD=∠BPE=90°,可得△BAD∽△BPE,即可得到![]() ,进而得出PB=
,进而得出PB=![]() ,PD=BD+PB=
,PD=BD+PB=![]() ;
;
(3)以A为圆心,AC长为半径画圆,当CE在⊙A下方与⊙A相切时,PD的值最小.
(1)∵△ABC和△ADE是有公共顶点的等腰直角三角形,∠BAC=∠DAE=90°,
∴BA=CA,DA=EA,∠BAC-∠DAC=∠DAE-∠DAC即∠BAD=∠CAE,
在△ABD和△ACE中,
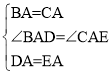
∴△ABD≌△ACE(SAS),
∴BD=CE;
故答案为:相等.
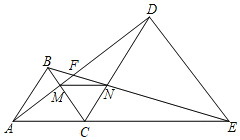
(2)作出旋转后的图形,若点C在AD上,如图2所示: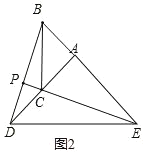
∵∠EAC=90°,
∴CE=![]() ,
,
∵∠PDA=∠AEC,∠PCD=∠ACE,
∴△PCD∽△ACE,
∴![]() ,即
,即![]()
∴PD=![]()
若点B在AE上,如图2所示:
∵∠BAD=90°,
∴Rt△ABD中,![]() ,BE=AEAB=2,
,BE=AEAB=2,
∵∠ABD=∠PBE,∠BAD=∠BPE=90°,
∴△BAD∽△BPE,
∴![]() ,即
,即![]() ,
,
解得PB=![]() ,
,
∴PD=BD+PB=![]() ,
,
综上可得,PD的长为![]() 或
或![]() .
.
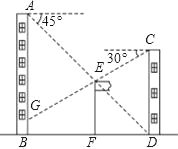
(2)如图3所示,以A为圆心,AC长为半径画圆,当CE在⊙A下方与⊙A相切时,PD的值最小 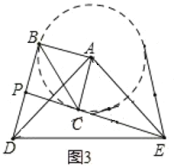
在Rt△PED中,PD=DEsin∠PED,因此锐角∠PED的大小直接决定了PD的大小.
当小三角形旋转到图中△ACB的位置时,
在Rt△ACE中,CE=![]() ,
,
在Rt△DAE中,DE=![]() ,
,
∵四边形ACPB是正方形,
∴PC=AB=3,
∴PE=3+4=7,
在Rt△PDE中,PD=![]() ,
,
即旋转过程中线段PD的最小值为1.

 阅读快车系列答案
阅读快车系列答案