题目内容
【题目】如图,在ABCD中,AB=6,AD=9,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE,垂足为G,BG= ![]() ,则△CEF的周长为( )
,则△CEF的周长为( ) 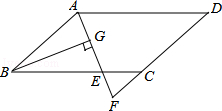
A.8
B.9.5
C.10
D.11.5
【答案】A
【解析】解:∵在ABCD中,AB=CD=6,AD=BC=9,∠BAD的平分线交BC于点E, ∴AB∥DC,∠BAF=∠DAF,
∴∠BAF=∠F,
∴∠DAF=∠F,
∴AD=FD,
∴△ADF是等腰三角形,
同理△ABE是等腰三角形,
AD=DF=9;
∵AB=BE=6,
∴CF=3;
∴在△ABG中,BG⊥AE,AB=6,BG= ![]() ,可得:AG=2,
,可得:AG=2,
又BG⊥AE,
∴AE=2AG=4,
∴△ABE的周长等于16,
又∵ABCD
∴△CEF∽△BEA,相似比为1:2,
∴△CEF的周长为8.
故选:A.
【考点精析】利用勾股定理的概念和平行四边形的性质对题目进行判断即可得到答案,需要熟知直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目




