��Ŀ����
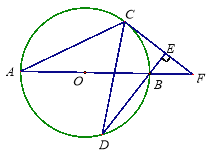
����Ŀ����ͼ���ı���ABCD�ǡ�O���ڽ��ı��Σ��Խ���AC��BD���ڵ�P���������5���۶ϣ���AB//CD����AP=PC����AB=CD���ܡ�BAD=��DCB����AD//BC��
(1)�����۶Ϣٺ͢���Ϊ��������֤�ı���ABCD�Ǿ��Σ�
(2)������ѡȡ�������Ƴ��ı���ABCDΪ���ε��۶ϣ��磺_________��_________��___________��________________(��֤��������ű�ʾ����)��
(3)��ѡȡ�۶Ϣۺ͢���Ϊ���������Ƴ��ı���ABCDΪ������?���ܣ������֤���������ܣ���ٷ���˵����

���𰸡���1��֤������������2���磺�ٺۣ͢���ںۣ͢���ۣܺ͢����ɼ���⣻��3�����ܣ����ɼ����.
��������
��1������Բ�ڽ��ı��ε����ʵõ���������������ɵ��ı���Ϊ��һ������ֱ�ǵ�ƽ���ı��μ����ж����Σ�
��2�����þ��ε������ж��������ɵõ����ۣ�
��3�����ܣ���Ϊһ��Ա�ƽ�У�����һ��Ա���ȵĻ��п����ǵ������Σ�
�⣺��AB//CD����AP=PC����A��=CD���ܡ�BAD=��DCB����AD//BC��
��1�����ı���ABCD�ǡ�O���ڽ��ı��Σ�
���BAD+��DCB=180����
�֡ߡ�BAD=��DCB��
���BAD=��DCB=90��
��AB//DC
���BAD+��ADC=180������ADC=90����
���ı���ABCD�Ǿ��Σ�
��2���磺��AB//CD�͢�AB=CD��
���ı���ABCD�У�
��AB//CD��AB=CD��
���ı���ABCD��ƽ���ı��Σ�
��AD��BC��
���BAD+��ABC=180�㣬
����BAD+��DCB=180����
���ABC=��DCB��
�ߡ�ABC+��DCB=180�㣬
���ABC=��DCB=90�㣬
��ƽ���ı���ABCD�Ǿ��Σ�
�磺��AP=PC�͢�AB=CD��
�ߡ�ACD=��ABD��AP=PC��AB=CD��
���ABP�ա�DCP��
��BP=DP��
���ı���ABCD��ƽ���ı��Σ�
��AD��BC��AB��CD��
���BAD+��ABC=180�㣬
����BAD+��DCB=180����
���ABC=��DCB��
�ߡ�ABC+��DCB=180�㣬
���ABC=��DCB=90�㣬
��ƽ���ı���ABCD�Ǿ��Σ�
�磺��AB=CD�͢ܡ�BAD=��DCB��
���ı���ABCD�ǡ�O���ڽ��ı��Σ�
���BAD+��DCB=180�㣬
���BAD=��DCB=90�㣬
�ߡ�BAC=��BDC��AB=CD����ABD=��ACD��
���ABP�ա�DCP��
��AP=CP��BP=DP��
���ı���ABCD��ƽ���ı��Σ�
�ߡ�BAD=��DCB=90�㣬
���ı���ABCD�Ǿ��Σ�
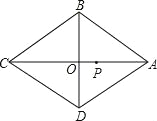
��3�����ܣ���ͼ��
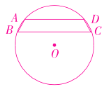
��AD//BC��AB=DC����B��90����
���ı���ABCD���Ǿ��Σ�