题目内容
要使直线y=kx+b经过二、一、四象限，则k________0，b________0．（填“＞”“＜”=）
＜ ＞
分析：根据图象在坐标平面内的位置关系确定k，b的取值范围，从而求解．
解答：由一次函数y=kx+b的图象经过二、一、四象限，
又由k＜0时，直线必经过二、四象限，故知k＜0．
再由图象过一、四象限，即直线与y轴正半轴相交，所以b＞0．
故答案是：＜，＞．
点评：本题主要考查一次函数图象在坐标平面内的位置与k、b的关系．解答本题注意理解：直线y=kx+b所在的位置与k、b的符号有直接的关系．k＞0时，直线必经过一、三象限．k＜0时，直线必经过二、四象限．b＞0时，直线与y轴正半轴相交．b=0时，直线过原点；b＜0时，直线与y轴负半轴相交．
分析：根据图象在坐标平面内的位置关系确定k，b的取值范围，从而求解．
解答：由一次函数y=kx+b的图象经过二、一、四象限，
又由k＜0时，直线必经过二、四象限，故知k＜0．
再由图象过一、四象限，即直线与y轴正半轴相交，所以b＞0．
故答案是：＜，＞．
点评：本题主要考查一次函数图象在坐标平面内的位置与k、b的关系．解答本题注意理解：直线y=kx+b所在的位置与k、b的符号有直接的关系．k＞0时，直线必经过一、三象限．k＜0时，直线必经过二、四象限．b＞0时，直线与y轴正半轴相交．b=0时，直线过原点；b＜0时，直线与y轴负半轴相交．
练习册系列答案
阅读快车系列答案
相关题目
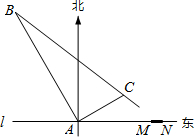60°，且与A相距
（1998•四川）已知一次函数y=kx+4的图象分别与直线x=2和x=6交于点A、B，且y随x的增大而增大，直线x=2和x=6又分别与x轴交于点D、C．