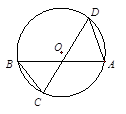题目内容
已知:如图, 是⊙
是⊙ 的直径,
的直径, 是⊙
是⊙ 外一点,过点
外一点,过点 作
作 的垂线
的垂线 ,交
,交 的延长线于点
的延长线于点 ,
, 的延长线与⊙
的延长线与⊙ 交于点
交于点 ,
, .
.

(1)求证: 是⊙
是⊙ 的切线;
的切线;
(2)若 ,⊙
,⊙ 的半径为
的半径为 ,求
,求 的长.
的长.
 是⊙
是⊙ 的直径,
的直径, 是⊙
是⊙ 外一点,过点
外一点,过点 作
作 的垂线
的垂线 ,交
,交 的延长线于点
的延长线于点 ,
, 的延长线与⊙
的延长线与⊙ 交于点
交于点 ,
, .
.
(1)求证:
 是⊙
是⊙ 的切线;
的切线;(2)若
 ,⊙
,⊙ 的半径为
的半径为 ,求
,求 的长.
的长.(1)证明见解析;(2) .
.
 .
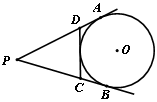
.试题分析:(1)连接OC,若要证明DC是⊙O的切线,则可转化为证明∠DCO=90°即可;
(2)设AD=k,则AE=
 ,ED=2k,利用勾股定理计算即可.
,ED=2k,利用勾股定理计算即可.试题解析:(1)证明:连结OC,

∵DE=DC,
∴∠4=∠E,
∵OA=OC,
∴∠1=∠2,
又∵∠2=∠3,
∴∠1=∠3,
∴∠4+∠1=∠E+∠3=90°,
∴DC是⊙O的切线;
(2)∵∠4=∠E,
∴
 ,
,设AD=k,则AE=
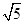 k,ED=2k,
k,ED=2k,∴DC=2k,
在Rt△OCD中,
由勾股定理得:OD2=DC2+OC2,
∴(
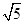 +k)2=(2k)2+
+k)2=(2k)2+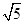 2,
2,∴k=0(舍),k=
 ,
,∴AE=
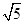 k=
k=
考点: 1.切线的判定;2.解直角三角形;3.勾股定理.

练习册系列答案
 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目

 )
)