题目内容
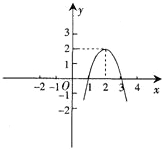
如图(1),在平面直角坐标系中二次函数y=-x2+bx+c的图象经过点A(1,-2),B(3,-1)
(1)求抛物线的解析式及顶点C的坐标;
(2)请问在y轴上是否存在点P,使得S△ABC=S△ABP?若存在,求出点P的坐标;若不存在,请说明理由;
(3)请在图(2)上用尺规作图的方式探究抛物线上是否存在点Q,使得△QAB是等腰三角形?若存在,请判断点Q共有几个可能的位置(保留作图痕迹);若不存在,请说明理由(不用证明).

(1)求抛物线的解析式及顶点C的坐标;
(2)请问在y轴上是否存在点P,使得S△ABC=S△ABP?若存在,求出点P的坐标;若不存在,请说明理由;
(3)请在图(2)上用尺规作图的方式探究抛物线上是否存在点Q,使得△QAB是等腰三角形?若存在,请判断点Q共有几个可能的位置(保留作图痕迹);若不存在,请说明理由(不用证明).

(1)由l2的解析式为y=-x2+bx+c,联立方程组:
解得得:b=
,c=-
,
则l2的解析式为y=-x2+
x-
=-(x-
)2-
.
点C的坐标为(
,-
).
(2)如答图1,过点A、B、C三点分别作x轴的垂线,垂足分别为D、E、F,
则AD=2,CF=
,BE=1,DE=2,DF=
,FE=
.
得:S△ABC=S梯形ABED-S梯形BCFE-S梯形ACFD=
.
延长BA交y轴于点G,直线AB的解析式为y=
x-
,则点G的坐标为(0,-
),设点P的坐标为(0,h),
①当点P位于点G的下方时,PG=-
-h,连接AP、BP,
则S△ABP=S△BPG-S△APG=-
-h,又S△ABC=S△ABP=
,得h=-
,点P的坐标为(0,-
).
②当点P位于点G的上方时,PG=
+h,同理h=-
,点P的坐标为(0,-
).
综上所述所求点P的坐标为(0,-
)或(0,-
)(7分)
(3)作图痕迹如答图2所示.
由图可知,
当以AB为腰以A为顶点时,以点A为圆心,以AB为半径画圆与抛物线交与Q1;
当以AB为腰以B为顶点时,以点b为圆心,以AB为半径画圆与抛物线交与Q2;
当以AB为底边时,作AB的垂直平分线交抛物线于Q3,Q4;
故满足条件的点有Q1、Q2、Q3、Q4,共4个可能的位置.(10分)

|
解得得:b=
| 9 |
| 2 |
| 11 |
| 2 |
则l2的解析式为y=-x2+
| 9 |
| 2 |
| 11 |
| 2 |
| 9 |
| 4 |
| 7 |
| 16 |
点C的坐标为(
| 9 |
| 4 |
| 7 |
| 16 |
(2)如答图1,过点A、B、C三点分别作x轴的垂线,垂足分别为D、E、F,
则AD=2,CF=
| 7 |
| 16 |
| 5 |
| 4 |
| 3 |
| 4 |
得:S△ABC=S梯形ABED-S梯形BCFE-S梯形ACFD=
| 15 |
| 16 |
延长BA交y轴于点G,直线AB的解析式为y=
| 1 |
| 2 |
| 5 |
| 2 |
| 5 |
| 2 |
①当点P位于点G的下方时,PG=-
| 5 |
| 2 |
则S△ABP=S△BPG-S△APG=-
| 5 |
| 2 |
| 15 |
| 16 |
| 55 |
| 16 |
| 55 |
| 16 |
②当点P位于点G的上方时,PG=
| 5 |
| 2 |
| 25 |
| 16 |
| 25 |
| 16 |
综上所述所求点P的坐标为(0,-
| 55 |
| 16 |
| 25 |
| 16 |
(3)作图痕迹如答图2所示.
由图可知,
当以AB为腰以A为顶点时,以点A为圆心,以AB为半径画圆与抛物线交与Q1;
当以AB为腰以B为顶点时,以点b为圆心,以AB为半径画圆与抛物线交与Q2;
当以AB为底边时,作AB的垂直平分线交抛物线于Q3,Q4;
故满足条件的点有Q1、Q2、Q3、Q4,共4个可能的位置.(10分)


练习册系列答案
相关题目
 经过点A(1,0)和点B(0,1).
经过点A(1,0)和点B(0,1).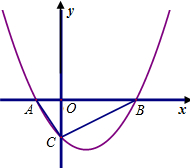
 顶点,O为坐标原点.若OA、OB(OA<OB)的长分别是方程x2-4x+3=0的两根,且∠DAB=45°.
顶点,O为坐标原点.若OA、OB(OA<OB)的长分别是方程x2-4x+3=0的两根,且∠DAB=45°. 点A与坐标原点重合,CB的延长线与y轴交于点F,且F(0,-6).
点A与坐标原点重合,CB的延长线与y轴交于点F,且F(0,-6).