题目内容
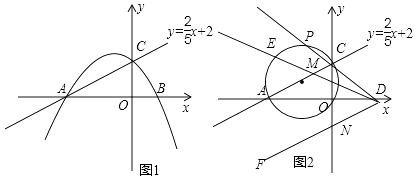
【题目】如图,直线AB交双曲线 ![]() 于A,B两点,交x轴于点C,且BC=
于A,B两点,交x轴于点C,且BC= ![]() AB,过点B作BM⊥x轴于点M,连结OA,若OM=3MC,S△OAC=8,则k的值为多少?
AB,过点B作BM⊥x轴于点M,连结OA,若OM=3MC,S△OAC=8,则k的值为多少? 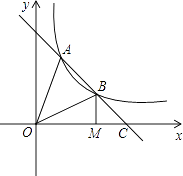
【答案】解:设B(a,b), ∵点B在函数y= ![]() 上,
上,
∴ab=k,且OM=a,BM=b,
∵OM=3MC,
∴MC= ![]() a,
a,
∴S△BOM= ![]() ab=
ab= ![]() k,S△BMC=
k,S△BMC= ![]() ×
× ![]() ab=
ab= ![]() ab=
ab= ![]() k,
k,
∴S△BOC=S△BOM+S△BMC= ![]() k+
k+ ![]() k=
k= ![]() k,
k,
∵BC= ![]() AB,不妨设点O到AC的距离为h,
AB,不妨设点O到AC的距离为h,
则 ![]() =
= 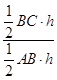 =
= ![]() =
= ![]() ,
,
∴S△AOB=2S△BOC= ![]() k,
k,
∴S△AOC=S△AOB+S△BOC= ![]() k+
k+ ![]() k=2k,
k=2k,
∵S△AOC=8.
∴2k=8,
∴k=4
【解析】设B坐标为(a,b),将B坐标代入反比例解析式求出得到ab=k,确定出OM与BM的长,根据OM=3MC,表示出MC长,进而表示出三角形BOM与三角形BMC的面积,两面积之和表示出三角形BOC面积,由BC为AB的一半,不妨设点O到AC的距离为h,求出三角形BOC与三角形AOB面积之比,确定出三角形AOC面积,利用反比例函数k的几何意义即可求出k的值.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目