题目内容
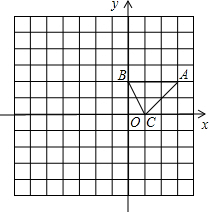 如图,△ABC在平面直角坐标系中,点A(3,2)、B(0,2)、C(1,0).解答问题:
如图,△ABC在平面直角坐标系中,点A(3,2)、B(0,2)、C(1,0).解答问题:(1)请按要求对△ABC作如下变换:
①将△ABC绕点O逆时针旋转90°得到△A1B1C1.
②以点O为位似中心,位似比为2:1,将△ABC在位似中心的异侧进行放大得到△A2B2C2;并写出点A1,A2的坐标:
(2)在△ABC内,点P的坐标为(a,b),在△A1B1C1中与之对应的点为Q,在△A2B2C2中与之对应的点为R.则S△PQR=
分析:(1)①把A、B、C各点绕点O逆时针旋转90°后,顺次连接得到的对应点即可;
②连接AO并延长到A2,使OA2=2OA,得到点A的对应点A2,同法得到其余点的对应点,连接即可,根据所在象限及距离坐标轴的距离可得相应坐标;
(2)S△PQR=
×PR×QO,把相关数值代入计算可得.
②连接AO并延长到A2,使OA2=2OA,得到点A的对应点A2,同法得到其余点的对应点,连接即可,根据所在象限及距离坐标轴的距离可得相应坐标;
(2)S△PQR=
| 1 |
| 2 |
解答: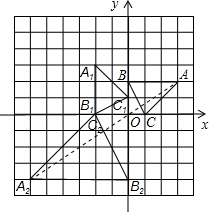 解:(1)如图,请按要求对△ABC作如下变换:
解:(1)如图,请按要求对△ABC作如下变换:
①画出△A1B1C1.
②画出△A2B2C2;
点A1的坐标为(-2,3),
点A2的坐标为(-6,-4).
故答案为(-2,3),(-6,-4);
(2)易得Q(-b,a),R(-2a,-2b),
PR=3
,OQ=
,OQ⊥OP,
∴S△PQR=
×PR×QO=
×3
×
=
(a2+b2).
 解:(1)如图,请按要求对△ABC作如下变换:
解:(1)如图,请按要求对△ABC作如下变换:①画出△A1B1C1.
②画出△A2B2C2;
点A1的坐标为(-2,3),
点A2的坐标为(-6,-4).
故答案为(-2,3),(-6,-4);
(2)易得Q(-b,a),R(-2a,-2b),
PR=3
| a2+b2 |
| a2+b2 |
∴S△PQR=
| 1 |
| 2 |
| 1 |
| 2 |
| a2+b2 |
| a2+b2 |
| 3 |
| 2 |
点评:考查旋转变换及位似变换;第二问中判断出△PQR的一边及这边上的高的长度是解决的难点.

练习册系列答案
相关题目
 24、如图,△ABC在平面直角坐标系内三顶点坐标分别为A(1,2),B(3,3),C(3,1)
24、如图,△ABC在平面直角坐标系内三顶点坐标分别为A(1,2),B(3,3),C(3,1)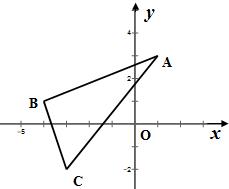 24、如图,△ABC在平面直角坐标系中A(1,3),B(-4,1),C(-3,2),以x轴为对称轴作对称变换,画出△A1B1C1,同时在x轴上找一点P,使P到A、B两点距离和最小?
24、如图,△ABC在平面直角坐标系中A(1,3),B(-4,1),C(-3,2),以x轴为对称轴作对称变换,画出△A1B1C1,同时在x轴上找一点P,使P到A、B两点距离和最小? 如图,△ABC在平面直角坐标系内三顶点坐标分别为A(1,2),B(3,3),C(3,1).
如图,△ABC在平面直角坐标系内三顶点坐标分别为A(1,2),B(3,3),C(3,1). 如图,△ABC在平面直角坐标系中,画出△ABC关于原点的对称图形△A1B1C1,并写出A1、B1、C1的坐标.
如图,△ABC在平面直角坐标系中,画出△ABC关于原点的对称图形△A1B1C1,并写出A1、B1、C1的坐标.