题目内容
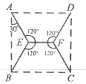
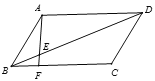
【题目】如图,平行四边形ABCD中,∠ABC=72°,AF⊥BC于点F,AF交BD于点E,若DE=2AB, 则∠AED=_______.
【答案】66°
【解析】
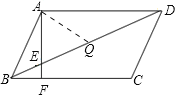
取DE的中点Q,连接AQ,根据平行四边形的性质求出FA⊥AD,根据三角形的内角和定理求出∠BAF,根据直角三角形斜边上的中线求出AQ=AB,推出∠ABD=2∠ADB,根据三角形的内角和定理求出∠ADB即可.
如图,取DE的中点Q,连接AQ,
∵平行四边形ABCD,
∴AD∥BC,
∵AF⊥BC,
∴FA⊥AD,
∴DE=2AQ=2DQ,
∵DE=2AB,
∴AQ=AB,
∴∠AQB=∠ABD,
∵AQ=DQ,
∴∠QAD=∠ADQ,
∴∠ABD=∠AQB=∠QAD+∠ADQ=2∠ADQ,
∵AF⊥BC,∠ABC=∠ADC=72°,
∴∠BAF=90°-72°=18°,
∵∠ABD+∠ADB+∠BAD=180°,
∴3∠ADB=180°-90°-18°=72°,
∴∠ADB=24°,
∵∠FAD=90°,
∴∠AED=180°-∠FAD-∠ADE=66°,
故答案为:66°.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】某公司实行年工资制,职工的年工资由基础工资、住房补贴和医疗费三项组成,具体规定如下:
项目 | 第一年的工资(万元) | 一年后的计算方法 |
基础工资 | 1 | 每年的增长率相同 |
住房补贴 | 0.04 | 每年增加0.04 |
医疗费 | 0.1384 | 固定不变 |
(1)设基础工资每年增长率为x,用含x的代数式表示第三年的基础工资为 万元;
(2)某人在公司工作了3年,他算了一下这3年拿到的住房补贴和医疗费正好是这3年基础工资总额的18 %,问基础工资每年的增长率是多少?