Question

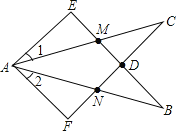
【题目】如图，在△ABC中，AM=CM，AD=CD，DM//BC，判断△CMB的形状，并说明理由．

Answer 1

【答案】△CMB是等腰三角形，理由见解析

【解析】

由等腰三角形的三线合一的性质可得∠AMD=∠CMD，再根据平行线的性质可得∠AMD=∠B，∠CMD=∠MCB，再根据等量代换可得∠B=∠MCB，根据等角对等边可得MC=MB，进而得到△CMB是等腰三角形．

在△AMC中，∵AM=CM，AD=CD，（已知），
∴∠AMD=∠CMD（等腰三角形三线合一），
∵DM∥BC（ 已知），
∴∠AMD=∠B（两直线平行，同位角相等），∠CMD=∠MCB（两直线平行，内错角相等），
∴∠B=∠MCB（等量代换），
∴MC=MB（等角对等边），
即△CMB是等腰三角形．