Question

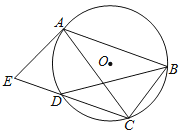
【题目】如图，四边形是的内接四边形，四边形两组对边的延长线分别相交于点，，且，，连接．

（1）求的度数；

（2）当的半径等于2时，请直接写出的长．(结果保留)

Answer 1

【答案】（1）45°；（2）π．

【解析】

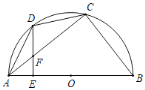
（1）根据圆内接四边形的性质得到∠DCE＝∠A，根据三角形外角性质得到∠EDF＝∠A＋50°，然后根据三角形内角和定理得到∠A＋50°＋∠A＋40°＝180°，从而解方程得到∠A的度数；

（2）连接OB、OD，如图，根据圆周角定理得到∠BOD＝2∠A＝90°，然后利用弧长公式计算的长．

（1）∵四边形ABCD是⊙O的内接四边形，

∴∠DCE=∠A．

∵∠EDF=∠A+∠F=∠A+50°，

而∠EDF+∠DCE+∠E=180°，

∴∠A+50°+∠A+40°=180°，

∴∠A=45°；

（2）连接OB、OD，如图，

∵∠BOD=2∠A=90°，

∴的长π．