题目内容
【题目】如图,在△ABC中,∠C=90°,AD平分∠CAB,交CB于点D,过点D作DE⊥AB于点E.
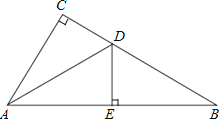
(1)求证:△ACD≌△AED;
(2)若∠B=30°,CD=1,求BD的长.
【答案】(1)证明见解析;(2)2.
【解析】
试题分析:(1)根据角平分线性质求出CD=DE,根据HL定理求出两三角形全等即可;
(2)求出∠DEB=90°,DE=1,根据含30度角的直角三角形性质求出即可.
试题解析:(1)∵AD平分∠CAB,DE⊥AB,∠C=90°,
∴CD=ED,∠DEA=∠C=90°,
∵在Rt△ACD和Rt△AED中
![]()
∴Rt△ACD≌Rt△AED(HL);
(2)∵DC=DE=1,DE⊥AB,
∴∠DEB=90°,
∵∠B=30°,
∴BD=2DE=2.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
【题目】九(1)班数学兴趣小组经过市场调查,整理出某种商品在第x(1≤x≤90)天的售价与销量的相关信息如下表:
时间x(天) | 1≤x<50 | 50≤x≤90 |
售价(元/件) | x+40 | 90 |
每天销量(件) | 200﹣2x | |
已知该商品的进价为每件30元,设销售该商品的每天利润为y元.
(1)求出y与x的函数关系式;
(2)问销售该商品第几天时,当天销售利润最大,最大利润是多少?
(3)该商品在销售过程中,共有多少天每天销售利润不低于4800元?请直接写出结果.