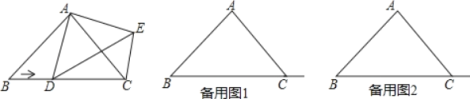
题目内容
【题目】填写推理的依据。
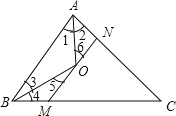
（1）已知：AB∥CD，AD∥BC。求证：∠B=∠D。
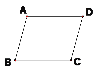
证明：∵AB∥CD，AD∥BC（ 已知 ）
∴∠A+∠B=180，∠A+∠D=180°（_______________________________）
∴∠B=∠D （___________________________）
（2）已知：DF∥AC，∠A=∠F。求证：AE∥BF。
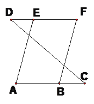
证明：∵DF∥AC （已知）
∴∠FBC=∠_______（_______________________________）
∵∠A=∠F（已知）
∴∠A=∠FBC （____________________）
∴AE∥FB （_____________________________）
【答案】两直线平行，同旁内角互补 等量代换 ∠F， 两直线平行,内错角相等 等量代换 同位角相等,两直线平行
【解析】
（1）根据平行线的特点，两直线平行，同旁内角互补，再根据等量代换即可得出答案，
（2）根据平行线的性质，两直线平行内错角相等，再根据等量代换得出∠A=∠FBC，再根据同位角相等，即可证明两直线平行，
(1)证明：∵AB∥CD，AD∥BC(已知)
∴
，(两直线平行,同旁内角互补)
∴∠B=∠D，(等量代换)
(2)证明：∵DF∥AC(已知)
∴∠FBC=∠F，(两直线平行,内错角相等)
∵∠A=∠F(已知)
∴∠A=∠FBC，(等量代换），
∴AE∥FB，(同位角相等,两直线平行)
练习册系列答案
阅读快车系列答案
相关题目
