Question

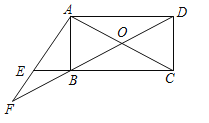
【题目】如图，点O是等边内一点，，，点D是等边△ABC外一点，∠OCD=60°，OC=OD，连接OD、AD．

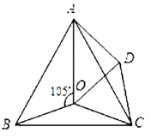
（1）求的度数（用含α的式子表示）

（2）求证：；

（3）探究：当α为多少度时，是等腰三角形．

Answer 1

【答案】（1）；（2）见解析；（3）或或

【解析】

（1）先证△OCD是等边三角形得到∠DOC=60°，根据，，即可得出答案；

（2）根据已知条件可得：BC=AC，DC=OC，∠BCA=∠OCD，再减去一个公共角∠OCA可得∠BCO=∠ACD，即可证出两个三角形全等；

（3）根据已知条件可得：，，，再分情况讨论：①；②；③，即可得出答案.

解：（1）∵，，

∴为等边三角形，

∴，

∵，﹐

∴；

（2）∵和均为等边三角形，

∴，，，

∴，

即．

在和中，

，

∴；

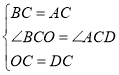（3）∵，

∴．

∵为等边三角形．

∴，

∴．

又由（1）可知，

∴，

∵是等腰三角形，

①，

即，

解得，

②，

即，

解得，

③，

即，

解得

综上：当或或时，是等腰三角形