题目内容
甲、乙两车分别从相距48千米的A地开往B地,到达B地后即刻(不停留)返回到A地.从A地开往B地时,乙车比甲车先出发一个小时,甲车的行速是乙车的3倍,结果甲车到达B地比乙车早0.6个小时.(1)求甲车的速度是多少千米/小时;
(2)从B地返回A地时,甲车(比乙车早出发0.6个小时)行速减为原来(从A地开往B地的行速)的一半,问乙车的行速至少为千米/小时才能比甲车先到A地?
分析:(1)设甲车的速度是x千米/小时,根据从A地开往B地时,乙车比甲车先出发一个小时,甲车的行速是乙车的3倍,结果甲车到达B地比乙车早0.6个小时,可列方程求解.
(2)设乙车为y千米/小时时,才能先到达A地,根据甲车(比乙车早出发0.6个小时)行速减为原来(从A地开往B地的行速)的一半,可列出不等式求解.
(2)设乙车为y千米/小时时,才能先到达A地,根据甲车(比乙车早出发0.6个小时)行速减为原来(从A地开往B地的行速)的一半,可列出不等式求解.
解答:解:(1)设甲车的速度是x千米/小时,
-
=0.6
x=60
经检验x=60是方程的解.
甲车的速度是60公里/小时.
(2)设乙车为y千米/小时时,才能先到达A地,
30×0.6+30•
≤48
y≥48.
故乙的速度至少为48公里/小时.
| 48 | ||
|
| 48 |
| x |
x=60
经检验x=60是方程的解.
甲车的速度是60公里/小时.
(2)设乙车为y千米/小时时,才能先到达A地,
30×0.6+30•
| 48 |
| y |
y≥48.
故乙的速度至少为48公里/小时.
点评:本题考查理解题意的能力,第一问根据时间做为等量关系列方程求解,第二问根据路程做为不等量关系列不等式求解.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目

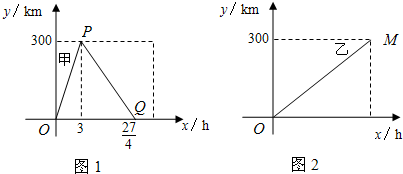
 (千米)与行驶时间x(小时)之间的函数关系式,写出自变量的取值范围;
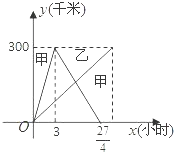
(千米)与行驶时间x(小时)之间的函数关系式,写出自变量的取值范围;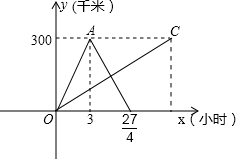 为了参观上海世博会,某公司安排甲、乙两车分别从相距300千米的上海、泰州两地同时出发相向而行,甲到泰州带客后立即返回,下图是它们离各自出发地的距离y(千米)与行驶时间x(小时)之间的函数图象.
为了参观上海世博会,某公司安排甲、乙两车分别从相距300千米的上海、泰州两地同时出发相向而行,甲到泰州带客后立即返回,下图是它们离各自出发地的距离y(千米)与行驶时间x(小时)之间的函数图象.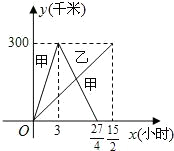 ,下图是它们离各自出发地的距离y(千米)与行驶时间x(小时)之间的函数图象.
,下图是它们离各自出发地的距离y(千米)与行驶时间x(小时)之间的函数图象.