题目内容
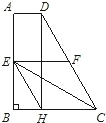 如图所示,在梯形ABCD中,AD∥BC,AB⊥BC,AD=1,BC=3,CD=4,EF是梯形的中位线,DH为梯形的高,则下列结论正确的有
如图所示,在梯形ABCD中,AD∥BC,AB⊥BC,AD=1,BC=3,CD=4,EF是梯形的中位线,DH为梯形的高,则下列结论正确的有①四边形EHCF为菱形;②∠BCD=60°;③S△BEH=
| 1 | 2 |
分析:根据已知对各个结论进行分析从而得到最后答案.
解答:解:①正确
∵EF=2,BH=AD=1
∴CH=2
∴即四边形EFCH是平行四边形
∵CF=2=EF
∴四边形EHCF为菱形;
②正确,在直角三角形CDH中,CH=2,CD=4,则∠CDH=30°,∴∠BCD=60°;
③正确,因为BH=
CH,所以S△BEH=
S△CEH;
④不正确,根据以上的证明只能得出以AB为直径的圆与CD相切于点G,而不切于点F,
因为EF=2,而圆的半径为根号3,
所以以AB为直径的圆不可能与点F相切.
④不正确,
∵以AB为直径的圆
∴圆心是E,半径是AB的一半
作EG⊥CD于G
∴∠ECG=30°
∴CE=2EG
∵在直角三角形BCE中,∠BCE=30°
∴CE=2BE=AB
∴AB=2EG
∴以AB为直径的圆与CD相切于点F;
故答案为:①②③.
∵EF=2,BH=AD=1
∴CH=2
∴即四边形EFCH是平行四边形
∵CF=2=EF
∴四边形EHCF为菱形;
②正确,在直角三角形CDH中,CH=2,CD=4,则∠CDH=30°,∴∠BCD=60°;
③正确,因为BH=
| 1 |
| 2 |
| 1 |
| 2 |
④不正确,根据以上的证明只能得出以AB为直径的圆与CD相切于点G,而不切于点F,
因为EF=2,而圆的半径为根号3,
所以以AB为直径的圆不可能与点F相切.
④不正确,
∵以AB为直径的圆
∴圆心是E,半径是AB的一半
作EG⊥CD于G
∴∠ECG=30°
∴CE=2EG
∵在直角三角形BCE中,∠BCE=30°
∴CE=2BE=AB
∴AB=2EG
∴以AB为直径的圆与CD相切于点F;
故答案为:①②③.
点评:此类题的综合性较强,要非常熟悉特殊四边形的性质以及直角三角形的性质和梯形的中位线定理.

练习册系列答案
 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
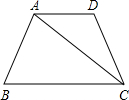 已知如图所示,在梯形ABCD中,AD∥BC,AB=AD=DC=8,∠B=60°,连接AC.
已知如图所示,在梯形ABCD中,AD∥BC,AB=AD=DC=8,∠B=60°,连接AC.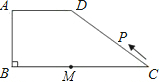 如图所示,在梯形ABCD中,AD∥BC,∠ABC=90°,AD=AB=6,BC=14,点M是线段BC上一定点,且MC=8.动点P从C点出发沿C?D?A?B的路线运动,运动到点B停止.在点P的运动过程中,使△PMC为等腰三角形的点P有
如图所示,在梯形ABCD中,AD∥BC,∠ABC=90°,AD=AB=6,BC=14,点M是线段BC上一定点,且MC=8.动点P从C点出发沿C?D?A?B的路线运动,运动到点B停止.在点P的运动过程中,使△PMC为等腰三角形的点P有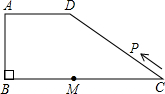 如图所示,在梯形ABCD中,AD∥BC,∠ABC=90°,AD=AB=6,BC=14,点M是线段BC上一定点,且MC=8.动点P从C点出发沿C→D→A→B的路线运动,运动到点B停止.在点P的运动过程中,使△PMC为等腰三角形的点P有几个?并求出相应等腰三角形的腰长.
如图所示,在梯形ABCD中,AD∥BC,∠ABC=90°,AD=AB=6,BC=14,点M是线段BC上一定点,且MC=8.动点P从C点出发沿C→D→A→B的路线运动,运动到点B停止.在点P的运动过程中,使△PMC为等腰三角形的点P有几个?并求出相应等腰三角形的腰长.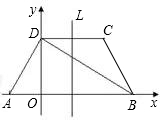 如图所示,在梯形ABCD中,已知AB∥CD,AD⊥DB,AD=DC=CB,AB=4,DO垂直于AB.则腰长是
如图所示,在梯形ABCD中,已知AB∥CD,AD⊥DB,AD=DC=CB,AB=4,DO垂直于AB.则腰长是 如图所示,在梯形ABCD中,AB∥DC,EF是梯形的中位线,AC交EF于G,BD交EF于H,以下说法错误的是( )
如图所示,在梯形ABCD中,AB∥DC,EF是梯形的中位线,AC交EF于G,BD交EF于H,以下说法错误的是( )