��Ŀ����
����Ŀ���Ķ����ϣ��ش��������⣺
������ѧϰ��������һ����Ҫ���ߣ��κ��������������������ϵĵ��ʾ�������ܹ��������ν�ϵķ������һЩ���⡣���磬�����������������϶�Ӧ�ĵ�֮��ľ�����������������IJ�ľ���ֵ��ʾ��
�������ϣ�������3��1��Ӧ������֮��ľ���Ϊ|31|=2��
��������,������5��2��Ӧ������֮��ľ���Ϊ|5(2)|=7��
�������ϣ�������2��3��Ӧ������֮��ľ���Ϊ|23|=5��
��������,������8��5��Ӧ������֮��ľ���Ϊ|8(5)|=3������
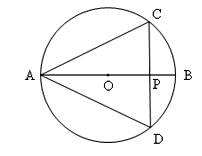
��ͼ1����������������a��Ӧ�ĵ�Ϊ��A��������b��Ӧ�ĵ�Ϊ��B��A��B����֮��ľ����ʾΪ|ab|��|ba|����Ϊ|AB|=|ab|=|ba|.

(1)������������10��5��Ӧ������֮��ľ������___��������������x��5��Ӧ������֮��ľ����ú�x��ʽ�ӱ�ʾΪ___����������������x��1��Ӧ������A��B֮��ľ���|AB|=2����x����___��
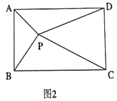
(2)��ͼ2����M��N��P�������ϵ����㣬��M��ʾ����Ϊ4����N��ʾ����Ϊ2������P��ʾ����Ϊx.

������P�ڵ�M��N֮�䣬��|x+2|+|x4|=___����|x+2|+|x4|�T10����x=___��
�ڸ����Ķ����ϼ���������Ľ����|x+2|+|x|+|x2|+|x4|����Сֵ����___.
���𰸡���1��5��|x+5|��1��3����2����6��6��4����8.
��������
��1�����ݾ���ֵ�Ķ��壺������������-10��-5��Ӧ������֮��ľ������5��������������x��-5��Ӧ������֮��ľ����ú�x��ʽ�ӱ�ʾΪ|x+5|����������������x��-1��Ӧ������A��B֮��ľ���|AB|=2����x����1��-3��
��2��������P�ڵ�M��N֮�䣬��|x+2|+|x-4|=6����|x+2|+|x-4|�T10����x=6��-4��
��|x+2|+|x|+|x-2|+|x-4|����Сֵ�������Сֵ=4-��-2��=6��
(1)���ݾ���ֵ�Ķ��壺
������������10��5��Ӧ������֮��ľ������5��
������������x��5��Ӧ������֮��ľ����ú�x��ʽ�ӱ�ʾΪ|x+5|��
A��B֮��ľ���|AB|=2����x����1��3��
(2)������P�ڵ�M��N֮�䣬��|x+2|+|x4|=6��
��|x+2|+|x4|�T10����x=6��4��
��|x+2|+|x|+|x2|+|x4|����Сֵ��
��x��4,2,0,4֮��������С,�����Сֵ=4(4)=8.
�ʴ�Ϊ��5��|x+5|��1��3��6��6��4��8.

 ��һ����ͬ���ɽ�����ϵ�д�
��һ����ͬ���ɽ�����ϵ�д� ������Ӧ���ϵ�д�
������Ӧ���ϵ�д� ��ʦ�㾦�ִʾ��ƪϵ�д�
��ʦ�㾦�ִʾ��ƪϵ�д�����Ŀ��Ϊ�����ѧ����д���ֵ���������ǿ�������ֵ���ʶ�������ٰ��ˡ�������д����������ѡ�κ���50��ѧ���μӾ�������50��ѧ��ͬʱ��д50�����֣���ÿ��ȷ��д��һ�����ֵ�1�֣����ݲ��Գɼ����Ƴ�����Ƶ���ֲ����Ͳ���Ƶ���ֲ�ֱ��ͼ��ͼ����
��� | �ɼ�x�� | Ƶ���������� |
��1�� | 25��x��30 | 4 |
��2�� | 30��x��35 | 6 |
��3�� | 35��x��40 | 14 |
��4�� | 40��x��45 | a |
��5�� | 45��x��50 | 10 |
����ͼ��������и��⣺
��1�������a��ֵ��
��2�����Ƶ���ֲ�ֱ��ͼ����������
��3�������Գɼ�������40��Ϊ���㣬�β��Ե��������Ƕ��٣�