题目内容
【题目】
活动1:在一只不透明的口袋中装有标号为1,2,3的3个小球,这些球除标号外都相同,充分搅匀,甲、乙、丙三位同学丙→甲→乙的顺序依次从袋中各摸出一个球(不放回),摸到1号球胜出,计算甲胜出的概率.(注:丙→甲→乙表示丙第一个摸球,甲第二个摸球,乙最后一个摸球)
活动2:在一只不透明的口袋中装有标号为1,2,3,4的4个小球,这些球除标号外都相同,充分搅匀,请你对甲、乙、丙三名同学规定一个摸球顺序: → → ,他们按这个顺序从袋中各摸出一个球(不放回),摸到1号球胜出,则第一个摸球的同学胜出的概率等于 ,最后一个摸球的同学胜出的概率等于 .
猜想:在一只不透明的口袋中装有标号为1,2,3,…,n(n为正整数)的n个小球,这些球除标号外都相同,充分搅匀,甲、乙、丙三名同学从袋中各摸出一个球(不放回),摸到1号球胜出,猜想:这三名同学每人胜出的概率之间的大小关系.
你还能得到什么活动经验?(写出一个即可)
【答案】(1)![]() ;(2)丙、甲、乙、
;(2)丙、甲、乙、![]() ,
,![]() ;(3)P(甲胜出)=P(乙胜出)=P(丙胜出),抽签是公平的,与顺序无关.(答案不唯一).
;(3)P(甲胜出)=P(乙胜出)=P(丙胜出),抽签是公平的,与顺序无关.(答案不唯一).
【解析】
试题分析:(1)画出树状图法,判断出甲胜出的概率是多少即可.
(2)首先对甲、乙、丙三名同学规定一个摸球顺序:丙→甲→乙,然后画出树状图法,判断出第一个摸球的丙同学和最后一个摸球的乙同学胜出的概率各等于多少即可.
(3)首先根据(1)(2),猜想这三名同学每人胜出的概率之间的大小关系为:P(甲胜出)=P(乙胜出)=P(丙胜出);然后总结出得到的活动经验为:抽签是公平的,与顺序无关.
试题解析:(1)如图1,
 ,
,
甲胜出的概率为:P(甲胜出)=![]() ;
;
(2)如图2,
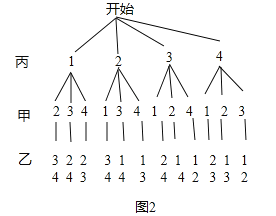 ,
,
对甲、乙、丙三名同学规定一个摸球顺序:丙→甲→乙,则第一个摸球的丙同学胜出的概率等于![]() ,最后一个摸球的乙同学胜出的概率也等于
,最后一个摸球的乙同学胜出的概率也等于![]() ,故答案为:丙、甲、乙、
,故答案为:丙、甲、乙、![]() ,
,![]() ;
;
(3)这三名同学每人胜出的概率之间的大小关系为:P(甲胜出)=P(乙胜出)=P(丙胜出).
得到的活动经验为:抽签是公平的,与顺序无关.(答案不唯一).

 优生乐园系列答案
优生乐园系列答案【题目】已知二次函数y=ax2+bx+c中,其函数y与自变量x之间的部分对应值如下表所示:
x | … | 0 | 1 | 2 | 3 | 4 | … |
y | … | 4 | 1 | 0 | 1 | 4 | … |
点A(x1,y1)、B(x2,y2)在函数的图象上,则当1<x1<2,3<x2<4时,y1与y2的大小关系正确的是( )
A.y1>y2B.y1<y2C.y1≥y2D.y1≤y2