题目内容
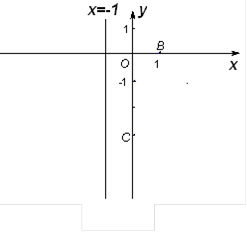
抛物线![]() 交x轴于A、B两点,交y轴于点C,已知抛物线的对称轴为直线x =-1,B(1,0),C(0,-3).
交x轴于A、B两点,交y轴于点C,已知抛物线的对称轴为直线x =-1,B(1,0),C(0,-3).
1.求二次函数![]() 的解析式;
的解析式;
2.求使y≥0的x的取值范围;
3.在抛物线对称轴上是否存在点P,使点C到点P和到直线![]() 的距离相等?若存在,求出点P坐标;若不存在,请说明理由
的距离相等?若存在,求出点P坐标;若不存在,请说明理由
1.∵ A、B两点关于对称轴![]() 对称,
对称,
∴ 点A(-3,0).
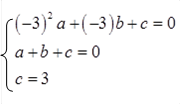 |
于是有
解得:![]() c=-3.
c=-3.
二次函数的解析式是: ![]()
2.由(1)知抛物线过A、B两点,又开口向上,
∴当x ≤-3或x≥1时,抛物线在x轴上方,
∴当x ≤-3或x≥1时,y≥0.
3.存在.
设点P 的坐标为(-1,![]() ),
),
则PC2=(![]() +3)2+12.
+3)2+12.
又点C到直线![]() 的距离为
的距离为![]() ,
,
∴(![]() +3)2+12=
+3)2+12=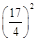 .
.
解得 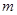 1=
1=![]() ,
,![]() 2=
2=![]() .
.
∴点P的坐标是(-1,![]() ),(-1,
),(-1,![]() )
)
解析:略

练习册系列答案
相关题目
 )两点.
)两点.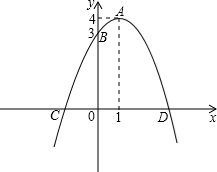 已知:如图,以A为顶点的抛物线交y轴于点B.
已知:如图,以A为顶点的抛物线交y轴于点B.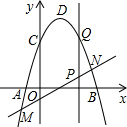 如图,在直角坐标系中,抛物线y=ax2+bx+c(a≠0)与x轴交于点A(-1,0)、B(3,0)两点,抛物线交y轴于点C(0,3),点D为抛物线的顶点.直线y=x-1交抛物线于点M、N两点,过线段MN上一点P作y轴的平行线交抛物线于点Q.
如图,在直角坐标系中,抛物线y=ax2+bx+c(a≠0)与x轴交于点A(-1,0)、B(3,0)两点,抛物线交y轴于点C(0,3),点D为抛物线的顶点.直线y=x-1交抛物线于点M、N两点,过线段MN上一点P作y轴的平行线交抛物线于点Q. M、N、B为顶点的三角形与△ABC相似,写出计算过程.
M、N、B为顶点的三角形与△ABC相似,写出计算过程.