题目内容
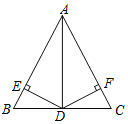
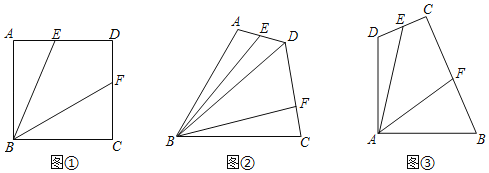
【题目】提出问题:(1)如图①,正方形ABCD中,点E,点F分别在边AD和边CD上,若正方形边长为4,DE+DF=4,则四边形BEDF的面积为 .
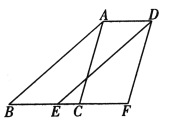
探究问题:(2)如图②,四边形ABCD,AB=BC=4,∠ABC=60°,∠ADC=120°,点E、F分别是边AD和边DC上的点,连接BE,BF,若ED+DF=3,BD=2![]() ,求四边形EBFD的面积;
,求四边形EBFD的面积;
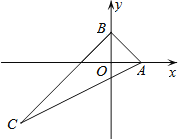
解决问题:(3)某地质勘探队为了进行资源助测,建立了如图③所示的一个四边形野外勘查基地,基地相邻两侧边界DA、AB长度均为4km,∠DAB=90°,由于勘测需要及技术原因,主勘测仪C与基地边缘D、B夹角为90°(∠DCB=90°),在边界CD和边界BC上分别有两个辅助勘测仪E和F,辅助勘测仪E和F与主勘测仪C的距离之和始终等于4km(CE+CF=4).为了达到更好监测效果,需保证勘测区域(四边形EAFC)面积尽可能大.请问勘测区域面积有没有最大值,如果有求出最大值,如果没有,请说明理由.
【答案】(1)8;(2)![]() ;(3)有,四边形EAFC的面积最大值为8km2
;(3)有,四边形EAFC的面积最大值为8km2
【解析】
提出问题:
(1)由四边形BEDF的面积=S△DEB+S△DFB,可求解;
探究问题:
(2)如图②,连接AC,过点B作BM⊥AD,BN⊥CD,通过证明点A,点B,点C,点D四点共圆,可得∠BAC=∠BDC=60°,∠ADB=∠ACB=60°,由直角三角形的性质可求BM=BN=![]() MD=
MD=![]() ,由四边形BEDF的面积=S△DEB+S△DFB,可求解;
,由四边形BEDF的面积=S△DEB+S△DFB,可求解;
解决问题:
(3)如图③,连接AC,BD,过点A作AM⊥CD,AN⊥BC,通过证明点A,点B,点C,点D四点共圆,且BD是直径,可得∠ACM=∠ABD=45°,∠ADB=∠ACB=45°,由直角三角形的性质可求AM=CM=![]() AC,AN=CN=
AC,AN=CN=![]() AC,由面积关系可求解.
AC,由面积关系可求解.
解:提出问题:
(1)如图①,连接BD,
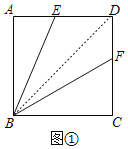
∵四边形BEDF的面积=S△DEB+S△DFB,
∴四边形BEDF的面积=![]() DE×AB+
DE×AB+![]() DF×BC=
DF×BC=![]() ×4×(DE+DF)=8,
×4×(DE+DF)=8,
故答案为:8;
探究问题:
(2)如图②,连接AC,过点B作BM⊥AD,BN⊥CD,

∵AB=BC=4,∠ABC=60°,
∴△ABC是等边三角形,
∴∠BAC=∠ACB=60°,
∵∠ABC=60°,∠ADC=120°,
∴点A,点B,点C,点D四点共圆,
∴∠BAC=∠BDC=60°,∠ADB=∠ACB=60°,
∵BM⊥AD,BN⊥CD,
∴∠MBD=30°,∠DBN=30°,且BD=2![]() ,
,
∴MD=DN=![]() BD=
BD=![]() ,
,
∴BM=BN=![]() MD=
MD=![]() ,
,
∵四边形BEDF的面积=S△DEB+S△DFB,
∴四边形BEDF的面积=![]() DE×BM+
DE×BM+![]() ×DF×BN=
×DF×BN=![]() ×
×![]() ×(DE+DF)=
×(DE+DF)=![]() ;
;
解决问题:
(3)如图③,连接AC,BD,过点A作AM⊥CD,AN⊥BC,
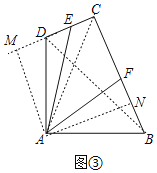
∵AB=AD=4km,∠DAB=90°,
∴∠ADB=∠ABD=45°,BD=4![]() km,
km,
∵∠DAB+∠BCD=90°+90°=180°,
∴点A,点B,点C,点D四点共圆,且BD是直径,
∴∠ACM=∠ABD=45°,∠ADB=∠ACB=45°,
∵AM⊥CD,AN⊥BC,
∴∠MAC=∠MCA=45°,∠NAC=∠ACN=45°,
∴AM=CM=![]() AC,AN=CN=
AC,AN=CN=![]() AC,
AC,
∵四边形EAFC的面积=S△ACE+S△AFC,
∴四边形EAFC的面积=![]() CE×AM+
CE×AM+![]() ×CF×AN=
×CF×AN=![]() ×AM×(CE+CF)=
×AM×(CE+CF)=![]() AC×4=
AC×4=![]() AC,
AC,
∴当AC为最大值时,四边形EAFC的面积有最大值,
∵AC是以BD为直径的圆中的弦,
∴AC的最大值为直径,
∴当AC=4![]() km,四边形EAFC的面积最大值为8km2.
km,四边形EAFC的面积最大值为8km2.