Question

【题目】某市的A地和B地秋季育苗，急需化肥分别为90吨和60吨，该市的C地和D地分别储存化肥100吨和50吨，全部调配给A地和B地，已知从C、D两地运化肥到A、B两地的运费（元/吨）如下表所示

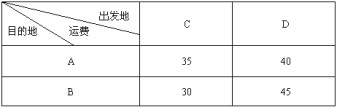
（1）设C地运到A地的化肥为吨，用含（吨）的代数式表示总运费W（元）

（2）求最低总运费，并说明总运费最低时的运送方案

（3）若总运费不少于5680元，共有几种方案？（化肥吨数取整数）

Answer 1

【答案】(1)、w=10x+4800（40≤x≤90）；(2)、C地的100吨化肥中40吨运往A地,60吨运往B地,D地的50吨化肥全部运往A地；(3)、三种方案

【解析】

试题分析：(1)、根据题意可得：D地运往A地(90－x)吨，C地运往B地(100－x)吨；D地运往B地(x－40)吨，根据总运费=各地的运费之和；(2)、根据函数的性质求出最小值；(3)、根据总运费以及第一题的取值范围得出x的取值范围，然后得出方案.

试题解析：(1)、∵C地运往A地的化肥为x吨

根据题意得：W=35x+40（90-x）+30（100-x）+45（x-40）=35x+3600-40x+3000-30x+45x-1800

=10x+4800（40≤x≤90）

(2)、当x=40时,W最小=10×40+4800=5200元,即运费最低时,x=40

∴100-x=100-40=60 90-x=90-40=50 x-40=40-40=0

答：总运费最低时的运送方案为：C地的100吨化肥中40吨运往A地,60吨运往B地,D地的50吨化肥全部运往A地.

(3)、10x+4800≥5680 x≥88 ∴88≤x≤90 适合的x可取88、89、90，

∴有3种方案