题目内容
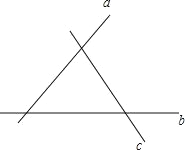
【题目】如图1,已知双曲线y= ![]() (k>0)与直线y=k′x交于A、B两点,点A在第一象限,试回答下列问题:
(k>0)与直线y=k′x交于A、B两点,点A在第一象限,试回答下列问题:
(1)若点A的坐标为(3,1),则点B的坐标为;当x满足:时, ![]() ≤k′x;
≤k′x;
(2)如图2,过原点O作另一条直线l,交双曲线y= ![]() (k>0)于P,Q两点,点P在第一象限.
(k>0)于P,Q两点,点P在第一象限.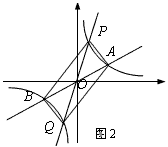
四边形APBQ一定是;
(3)若点A的坐标为(3,1),点P的横坐标为1,求四边形APBQ的面积.
(4)设点A,P的横坐标分别为m,n,四边形APBQ可能是矩形吗?可能是正方形吗?若可能,直接写出m,n应满足的条件;若不可能,请说明理由.
【答案】
(1)(﹣3,﹣1);﹣3≤x<0或x≥3
(2)平行四边形
(3)
∵点A的坐标为(3,1),
∴k=3×1=3,∴反比例函数的解析式为y= ,∵点P的横坐标为1,∴点P的纵坐标为3,∴点P的坐标为(1,3),
由双曲线关于原点对称可知,点Q的坐标为(﹣1,﹣3),点B的坐标为(﹣3,﹣1),
如图2,过点A、B分别作y轴的平行线,过点P、Q分别作x轴的平行线,分别交于C、D、E、F,
则四边形CDEF是矩形,
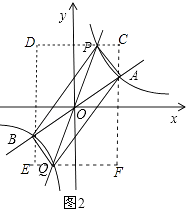
CD=6,DE=6,DB=DP=4,CP=CA=2,
则四边形APBQ的面积=矩形CDEF的面积﹣△ACP的面积﹣△PDB的面积﹣△BEQ的面积﹣△AFQ的面积
=36﹣2﹣8﹣2﹣8=16.
(4)
解:mn=k时,四边形APBQ是矩形,不可能是正方形,理由:当AB⊥PQ时四边形APBQ是正方形,此时点A、P在坐标轴上,由于点A,P可能达到坐标轴故不可能是正方形,即∠POA≠90°.因为mn=k,易知P、A关于直线y=x对称,所以PO=OA=OB=OQ,所以四边形APBQ是矩形.
【解析】解:(1)∵A、B关于原点对称,A(3,1),
∴点B的坐标为(﹣3,﹣1).由图象可知,当﹣3≤x<0或x≥3时, ![]() ≤k′x.
≤k′x.
故答案为(﹣3,﹣1),﹣3≤x<0或x≥3;(2)∵A、B关于原点对称,P、Q关于原点对称,
∴OA=OB,OP=OQ,∴四边形APBQ是平行四边形.故答案为:平行四边形;
=36﹣2﹣8﹣2﹣8=16.
(1)根据正比例函数与反比例函数的图象的交点关于原点对称,即可解决问题,利用图象根据正比例函数的图象在反比例函数的图象的上方,即可确定自变量x的范围.(2)利用对角线互相平分的四边形是平行四边形证明即可.(3)利用分割法求面积即可.(3)根据矩形的性质、正方形的性质即可判定.

 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案【题目】(1)填表:
a | 0.000 001 | 0.001 | 1 | 1 000 | 1 000 000 |
| 0.01 | 0.1 | 1 | 10 | 100 |
(2)由上表你发现了什么规律?请用语言叙述这个规律:被开方数扩大_____;
(3)根据你发现的规律填空:
①已知![]() =1.442,则
=1.442,则![]() =______,
=______,![]() =______;
=______;
②已知![]() =0.076 97,则=______.
=0.076 97,则=______.