题目内容
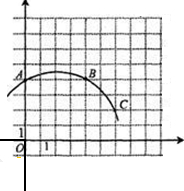 如图,在正方形网格中建立直角坐标系,一条圆弧经过网格点A、B、C,设此弧所在圆的圆心为D点.扇形DAC是某一个圆锥的侧面展开图,则该圆锥的底面半径为
如图,在正方形网格中建立直角坐标系,一条圆弧经过网格点A、B、C,设此弧所在圆的圆心为D点.扇形DAC是某一个圆锥的侧面展开图,则该圆锥的底面半径为分析:根据题意,显然要首先确定点D的位置.根据“弦的垂直平分线必过圆心”,作弦AB和BC的垂直平分线,即发现D(2,0).则扇形DAC的半径是2
.运用三角形全等的知识可以证明∠ADC=90°,然后利用弧长公式计算即可.
| 5 |
解答:解:根据扇形的弧长公式,
求得扇形的弧长是
×2
=
π,
扇形的弧长即圆锥的底面周长,
所以圆锥的底面半径是
.
求得扇形的弧长是
| 90π |
| 180 |
| 5 |
| 5 |
扇形的弧长即圆锥的底面周长,
所以圆锥的底面半径是
| ||
| 2 |
点评:此题的难点在于确定圆心的位置和计算扇形的圆心角度数.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
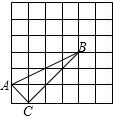 如图,在正方形网格中有△ABC,则sin∠ABC的值等于( )
如图,在正方形网格中有△ABC,则sin∠ABC的值等于( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
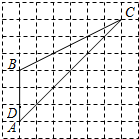 如图,在正方形网格中,点A、B、C、D都是格点,点E是线段AC上任意一点.如果AD=1,那么当AE=
如图,在正方形网格中,点A、B、C、D都是格点,点E是线段AC上任意一点.如果AD=1,那么当AE=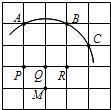 6、如图,在5×5正方形网格中,一条圆弧经过A,B,C三点,那么这条圆弧所在圆的圆心是( )
6、如图,在5×5正方形网格中,一条圆弧经过A,B,C三点,那么这条圆弧所在圆的圆心是( )
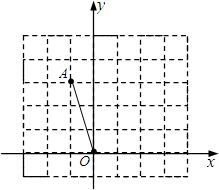 如图,在正方形网格中建立平面直角坐标系,格点O为原点,格点A的坐标为(-1,3).
如图,在正方形网格中建立平面直角坐标系,格点O为原点,格点A的坐标为(-1,3).