题目内容
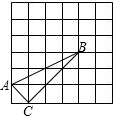如图，在正方形网格中有△ABC，则sin∠ABC的值等于（ ）A、
| ||||
B、
| ||||
C、
| ||||
D、
|
分析：首先利用勾股定理分别算出AB、BC、AC的长度，再利用勾股定理的逆定理得出∠ACB=90°，最后根据锐角三角函数的定义求出sin∠ABC的值．
解答：解：∵AB=
，BC=
，AC=
，
∴AB2=BC2+AC2，
∴∠ACB=90°．
∴sin∠ABC=
=
=
．
故选B．
| 20 |
| 18 |
| 2 |
∴AB2=BC2+AC2，
∴∠ACB=90°．
∴sin∠ABC=
| AC |
| AB |
| ||
|
| ||
| 10 |
故选B．
点评：本题主要考查了勾股定理和它的逆定理以及锐角三角函数的定义．
在直角三角形中，锐角的正弦为对边比斜边．
在直角三角形中，锐角的正弦为对边比斜边．
练习册系列答案
阅读快车系列答案
相关题目
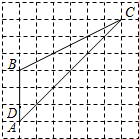如图，在正方形网格中，点A、B、C、D都是格点，点E是线段AC上任意一点．如果AD=1，那么当AE=
6、如图，在5×5正方形网格中，一条圆弧经过A，B，C三点，那么这条圆弧所在圆的圆心是（ ）
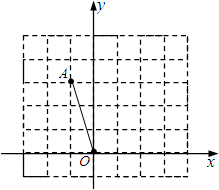如图，在正方形网格中建立平面直角坐标系，格点O为原点，格点A的坐标为（-1，3）．