Question

【题目】如图，四边形ABCD中，AB=15，BC=12，CD=16，AD=25，且∠C=90°，则四边形ABCD的面积是（ ）
A.246
B.296
C.592
D.以上都不对

Answer 1

【答案】A
【解析】解：连接BD．

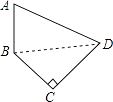
∵∠C=90°，BC=12，CD=16，

∴BD= =20，

在△ABD中，∵BD=20，AB=15，DA=25，

152+202=252，

即AB2+BD2=AD2，

∴△ABD是直角三角形．

∴S四边形ABCD=S△ABD+S△BCD

= ABBD+ BCCD

= ×15×20+ ×12×16

=150+96

=246．

故选：A．

【考点精析】掌握勾股定理的概念和勾股定理的逆定理是解答本题的根本，需要知道直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2；如果三角形的三边长a、b、c有下面关系：a2+b2=c2，那么这个三角形是直角三角形．