题目内容
 如图,∠AOB=45°,过OA上到点O的距离分别为1,3,5,7,9,11,的点作OA的垂线与OB相交,得到并标出一组黑色梯形,它们的面积分别为S1,S2,S3,S4,…,观察图中的规律,求出第10个黑色梯形的面积S10=
如图,∠AOB=45°,过OA上到点O的距离分别为1,3,5,7,9,11,的点作OA的垂线与OB相交,得到并标出一组黑色梯形,它们的面积分别为S1,S2,S3,S4,…,观察图中的规律,求出第10个黑色梯形的面积S10=分析:仔细观察可发现规律:第n个黑色梯形的上底=1+(n-1)×4,下底=1+(n-1)×4+2,然后按此公式求得上下底,再利用面积公式计算面积就行了.
解答:解:解法①:从图中可以看出,第一个黑色梯形的上底为1,下底为3,第2个黑色梯形的上底为5=1+4,下底为7=1+4+2,第3个黑色梯形的上底为9=1+2×4,下底为11=1+2×4+2,则第n个黑色梯形的上底=1+(n-1)×4,下底=1+(n-1)×4+2,
∴第10个黑色梯形的上底=1+(10-1)×4=37,下底=1+(10-1)×4+2=39,
∴第10个黑色梯形面积S10=
×(37+39)×2=76.
解法②根据图可知:
S1=4,
S2=12,
S3=20,
以此类推得Sn=8n-4,
S10=8×10-4=76.
∴第10个黑色梯形的上底=1+(10-1)×4=37,下底=1+(10-1)×4+2=39,
∴第10个黑色梯形面积S10=
| 1 |
| 2 |
解法②根据图可知:
S1=4,
S2=12,
S3=20,
以此类推得Sn=8n-4,
S10=8×10-4=76.
点评:本题是找规律题,找到第n个黑色梯形的上底=1+(n-1)×4,下底=1+(n-1)×4+2是解题的关键.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
 如图,∠AOB=45°,过OA上到点O的距离分别为1,2,3,4,5 …的点作OA的垂线与OB相交,再按一定规律标出一组如图所示的黑色梯形.设前n个黑色梯形的面积和为Sn.
如图,∠AOB=45°,过OA上到点O的距离分别为1,2,3,4,5 …的点作OA的垂线与OB相交,再按一定规律标出一组如图所示的黑色梯形.设前n个黑色梯形的面积和为Sn.| n | 1 | 2 | 3 | … |
| Sn | … |
(2)已知Sn与n之间满足一个二次函数关系,试求出这个二次函数的解析式.
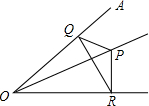 如图,∠AOB=45°,角内有点P,PO=10,在角的两边上有两点Q,R(均不同于O点),则△PQR的周长的最小值为
如图,∠AOB=45°,角内有点P,PO=10,在角的两边上有两点Q,R(均不同于O点),则△PQR的周长的最小值为 如图,∠AOB=45°,OC平分∠AOB,点M在OB上,且OM=
如图,∠AOB=45°,OC平分∠AOB,点M在OB上,且OM= 如图,∠AOB=45°,在OA上截取OA1=1,OA2=3,OA3=5,OA4=7,OA5=9,…,过点A1、A2、A3、A4、A5分别作OA的垂线与OB相交,得到并标出一组阴影部分,它们的面积分别为S1,S2,S3,….观察图中的规律,第n个阴影部分的面积Sn为( )
如图,∠AOB=45°,在OA上截取OA1=1,OA2=3,OA3=5,OA4=7,OA5=9,…,过点A1、A2、A3、A4、A5分别作OA的垂线与OB相交,得到并标出一组阴影部分,它们的面积分别为S1,S2,S3,….观察图中的规律,第n个阴影部分的面积Sn为( )