题目内容
【题目】如图，在
中，
，
，
，D为AC中点，P为AB上的动点，将P绕点D逆时针旋转
得到
，连
，则线段的最小值为
A. 
B. 
C. 2 D. 
【答案】C
【解析】过P'作P'E⊥AC于E，由旋转的性质及同角的余角相等，再用AAS判断出△DAP≌△P'ED，根据全等三角形对应边相等得出P'E=AD=2，当AP=DE=2时，DE=DC，即点E与点C重合，此时CP'=EP'=2，故线段CP′的最小值为2.
解：如图所示，过P'作P'E⊥AC于E，
则∠A=∠P'ED=90°，
由旋转可得，DP=P'D，∠PDP'=90°，
∴∠ADP=∠EP'D，
在△DAP和△P'ED中，
，
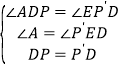∴△DAP≌△P'ED（AAS），
∴P'E=AD=2，
∴当AP=DE=2时，DE=DC，即点E与点C重合，
此时CP'=EP'=2，
∴线段CP′的最小值为2.
故选：C
练习册系列答案
相关题目
