题目内容
(10分)如图,CD∥AB,∠ABC,∠BCD的角平分线交于E点,且E在AD上,CE交BA的延长线于F点。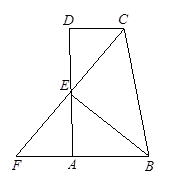
【小题1】(1)BE与CF互相垂直吗?若垂直,请说明理由;
【小题2】(2)若CD=3,AB=4,求BC的长.
【小题1】解:(1)垂直. ……………………………………… … (1分)
… (1分)
∵CD∥AB,
∴∠ABC+∠BCD=180°, ………………………………………… (2分)
∵∠ABC,∠BCD的角平分线交于E点,
∴∠ABE=∠EBC,∠DCE=∠ECB,
∴∠EBC+∠ECB= 1/2∠ABC+ 1/2∠BCD= 1/2(∠ABC+∠BCD)=90°,
∴∠CEB=90°,
∴BE与CF互相垂直.
【小题2】(2)∵∠CEB=90°,
∴∠FEB=90°,
∵∠FBE=∠CBE,BE=BE,
∴△FBE≌△CBE,
∴BF=BC ,EF=EC, ………………………………………… (2分)
,EF=EC, ………………………………………… (2分)
∵CD∥AB,
∴∠DCE=∠AFE,
∵∠FEA=∠CED,
∴△DCE≌△AFE, ………………………………………… (2分)
∴DC=AF,
∵CD=3,AB=4,BF=AF+AB,
∴BF=BC=7.
解析

练习册系列答案
相关题目
 18、如图,CD⊥AB于D,DE∥BC,∠1=∠2,则FG与AB的位置关系是
18、如图,CD⊥AB于D,DE∥BC,∠1=∠2,则FG与AB的位置关系是 26、如图,CD⊥AB,EF⊥AB,垂足分别为D、F,∠1=∠2,试判断DG与BC的位置关系,并说明理由.
26、如图,CD⊥AB,EF⊥AB,垂足分别为D、F,∠1=∠2,试判断DG与BC的位置关系,并说明理由. 12、如图,CD⊥AB,D为垂足,∠CDE=30°,则∠BDE=
12、如图,CD⊥AB,D为垂足,∠CDE=30°,则∠BDE=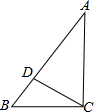 如图,CD⊥AB于D,AC=20,BC=15,DB=9.
如图,CD⊥AB于D,AC=20,BC=15,DB=9. 已知:如图,CD⊥AB,交点为点D,BE⊥AC,交点为点E,BE、CD交于点O,且AO平分∠BAC.试问:OB与OC有何大小关系,并说明理由.
已知:如图,CD⊥AB,交点为点D,BE⊥AC,交点为点E,BE、CD交于点O,且AO平分∠BAC.试问:OB与OC有何大小关系,并说明理由.