题目内容
 已知:如图,CD⊥AB,交点为点D,BE⊥AC,交点为点E,BE、CD交于点O,且AO平分∠BAC.试问:OB与OC有何大小关系,并说明理由.
已知:如图,CD⊥AB,交点为点D,BE⊥AC,交点为点E,BE、CD交于点O,且AO平分∠BAC.试问:OB与OC有何大小关系,并说明理由.分析:由于CD⊥AB,BE⊥AC,∠BOD和∠COE是对顶角,利用直角三角形的性质、等角的余角相等易证∠B=∠C,而AO平分∠BAC,利用角平分线的性质可得∠BAO=∠CAO,图中隐含的条件是AO=AO,利用AAS可证△AOB≌△AOC,于是OB=OC.
解答:解:OB=OC.理由如下:
∵CD⊥AB,BE⊥AC,
∴∠BDO=∠CEO=90°,
∴∠B+∠BOD=∠C+∠COE=90°,
∵∠BOD=∠COE,
∴∠B=∠C,
∵AO平分∠BAC,
∴∠BAO=∠CAO,
在△AOB和△AOC中,
,
∴△AOB≌△AOC(AAS),
∴OB=OC.
∵CD⊥AB,BE⊥AC,
∴∠BDO=∠CEO=90°,
∴∠B+∠BOD=∠C+∠COE=90°,
∵∠BOD=∠COE,
∴∠B=∠C,
∵AO平分∠BAC,
∴∠BAO=∠CAO,
在△AOB和△AOC中,
|
∴△AOB≌△AOC(AAS),
∴OB=OC.
点评:本题考查了全等三角形的判定和性质,解题的关键是先证明∠B=∠C,以及注意图中隐含的条件.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 4、已知:如图,CD⊥AB,BE⊥AC,垂足分别为D、E,BE、CD相交于O点,∠1=∠2.图中全等的三角形共有( )
4、已知:如图,CD⊥AB,BE⊥AC,垂足分别为D、E,BE、CD相交于O点,∠1=∠2.图中全等的三角形共有( ) 22、已知,如图,CD平分∠ACB,AC∥DE,CD∥EF,求证:EF平分∠DEB.
22、已知,如图,CD平分∠ACB,AC∥DE,CD∥EF,求证:EF平分∠DEB.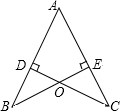 已知:如图,CD⊥AB于点D,BE⊥AC于点E,BE与CD交于点O,且BD=CE.
已知:如图,CD⊥AB于点D,BE⊥AC于点E,BE与CD交于点O,且BD=CE. 已知:如图,CD⊥AB于点D,BE⊥AC于点E,BE、CD交于点O,且AO平分∠BAC.那么OB与OC相等吗?谈谈你的理由.
已知:如图,CD⊥AB于点D,BE⊥AC于点E,BE、CD交于点O,且AO平分∠BAC.那么OB与OC相等吗?谈谈你的理由. 已知:如图AB∥CD,CE平分∠ACD,∠A=110°,则∠ECD等于
已知:如图AB∥CD,CE平分∠ACD,∠A=110°,则∠ECD等于