题目内容
如图,已知O(0,0)、A(4,0)、B(4,3).动点P从O点出发,以每秒3个单位的速度,沿△OAB的边0A、AB、B0作匀速运动;动直线l从AB位置出发,以每秒1个单位的速度向x轴负方向作匀速平移运动.若它们同时出发,运动的时间为t秒,当点P运动到O时,它们都停止运动.
(1)当P在线段OA上运动时,求直线l与以P为圆心、1为半径的圆相交时t的取值范围;
(2)当P在线段AB上运动时,设直线l分到与OA、OB交于C、D,试问:四边形CPBD是否可能为菱形?若能,求出此时t的值;若不能,请说明理由,并说明如何改变直线l的出发时间,使得四边形CPBD会是菱形.
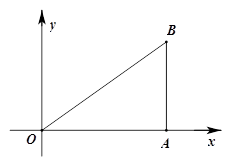
(1)当点P在线段OA上时,P(3t,0), …………………………………1分
⊙P与x轴的两交点坐标分别为(3t-1,0)、(3t+1,0),直线l为x=4-t,
若直线l与⊙P相交,则. ………………………………………3分
解得<t<. ………………………………………5分
(2)点P与直线l运动t秒时,AP=3t-4,AC=t,若要四边形CPBD为菱形,则
CP∥OB,
∴∠PCA=∠BOA,∴Rt△APC∽△ABO,∴=,∴=,解得t=………6分
此时,AP=,AC=,∴PC=,而PB=7-3t=≠PC,故四边形CPBD不可能是菱形 …………………………………………7分
(上述方法不唯一,只要推出矛盾即可)
现改变直线l的出发时间,高直线l比点P晚出发a秒,
若四边形CBPD为菱形,则CP∥OB,
∴Rt△APC∽△ABO,∴==,∴==,
即,解得
只要直线l比点P晚出发秒,则当点P运动秒时,四边形CPBD就是菱形……………10分
解析:略

 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案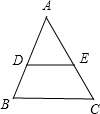 如图,已知:DE∥BC,AB=14,AC=18,AE=10,则AD的长为( )
如图,已知:DE∥BC,AB=14,AC=18,AE=10,则AD的长为( )A、
| ||
B、
| ||
C、
| ||
D、
|
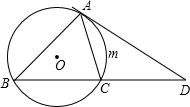 =2,∠ADC=30°
=2,∠ADC=30°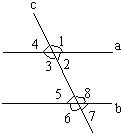 30、如图,已知直线a,b与直线c相交,下列条件中不能判定直线a与直线b平行的是( )
30、如图,已知直线a,b与直线c相交,下列条件中不能判定直线a与直线b平行的是( )
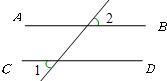 13、如图,已知直线AB∥CD,∠1=50°,则∠2=
13、如图,已知直线AB∥CD,∠1=50°,则∠2=