题目内容
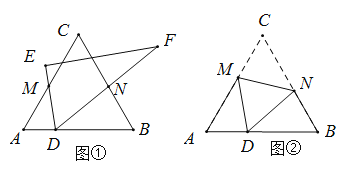
【题目】如图,![]() 中,内切圆O和边
中,内切圆O和边![]() 、
、![]() 、
、![]() 分别相切于点D、E、F,则以下四个结论中,错误的结论是( )
分别相切于点D、E、F,则以下四个结论中,错误的结论是( )
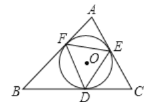
A.点O是![]() 的外心B.
的外心B.![]()
C.![]() D.
D.![]()
【答案】D
【解析】
首先连接如图所示的辅助线.采用排除法,证明A、B、C选项,从而错误的选择D.在证明中运用弦切角定理,直角三角形的两直角边所对的角互余.
解:A、∵点O是△ABC的内心
∴OE=OD=OF
∴点O也是△DEF的外心
∴该选项正确;
B、∵∠AFE=∠EDF(弦切角定理)
在Rt△BOD中,∠BOD=90°-∠OBD=90°![]() ∠B
∠B
同理∠COD=90°![]() ∠C
∠C
∴∠BOC=∠BOD+∠COD=180°![]() (∠C+∠B),即∠BOC=180°
(∠C+∠B),即∠BOC=180°![]() (∠C+∠B)
(∠C+∠B)
在四边形MOND中,OM⊥FD,ON⊥ED
∴∠BOC+∠MDN=180°
∴∠MDN=180°-∠BOC,即∠BOC=180°-∠EDF
∴∠AFE=![]() (∠B+∠C)
(∠B+∠C)
故该选项正确;
C、∵∠AFE=∠EDF(弦切角定理),
∵在Rt△AFO中,∠AFE=90°-∠FAO=90°-![]() ∠A,
∠A,
由上面B选项知∠MDN=180°-∠BOC=180°-(90°-![]() ∠A)=90°+
∠A)=90°+![]() ∠A,
∠A,
故该选项正确;
故选:D.

 阅读快车系列答案
阅读快车系列答案【题目】在建设港珠澳大桥期间,大桥的规划选线须经过中华白海豚国家级白然保护区—区域![]() 或区域
或区域![]() .为实现白海豚“零伤亡,不搬家”的目标,需合理安排施工时间和地点,为此,海豚观察员在相同条件下连续出海
.为实现白海豚“零伤亡,不搬家”的目标,需合理安排施工时间和地点,为此,海豚观察员在相同条件下连续出海![]() 天,在区域
天,在区域![]() 、
、![]() 两地对中华白海豚的踪迹进行了观测和统计,过程如下,请补充完整.(单位:头)
两地对中华白海豚的踪迹进行了观测和统计,过程如下,请补充完整.(单位:头)
(收集数据)
连续![]() 天观察中华白海豚每天在区域
天观察中华白海豚每天在区域![]() 、区域
、区域![]() 出现的数目情况,得到统计结果,并按从小到大的顺序排列如下:
出现的数目情况,得到统计结果,并按从小到大的顺序排列如下:
区域 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
区域 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(整理、描述数据)
(1)按如下数段整理、描述这两组数据,请补充完整:
海豚数 |
|
|
|
|
|
区域 |
|
|
| _________ | _________ |
区域 |
|
|
|
|
|
(2)两组数据的平均数、中位数,众数如下所示:
观测点 | 平均数 | 中位数 | 众数 |
区域 |
|
|
|
区域 |
|
|
|
请填空:上表中中位数![]() _______,,众数
_______,,众数![]() ______;
______;
(3)规划者们选择了区域![]() 为大桥的必经地,为减少施工对白海豚的影响,合理安排施工时间,估计在接下来的
为大桥的必经地,为减少施工对白海豚的影响,合理安排施工时间,估计在接下来的![]() 天施工期内,区域
天施工期内,区域![]() 大约有多少天中华白海豚出现的数目在
大约有多少天中华白海豚出现的数目在![]() 的范围内?
的范围内?