题目内容
【题目】如图，在平面直角坐标系中，已知
， 
， 
三点，其中
满足关系式
.
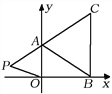
（1）求
的值;
（2）如果在第二象限内有一点
，那么请用含
的式子表示四边形
的面积；
（3）在（2）的条件下，是否存在点
，使四边形
的面积与三角形
的面积相等？若存在，求出点
的坐标；若不存在，请说明理由.
【答案】（1）a=2，b=3，c=4；（2） 
；（3）存在，点P的坐标为
.
【解析】试题分析：（1）根据非负数的性质：若几个非负数的和为0，这几个数均为0，即可求得结果；
（2）过点p作PD⊥y轴于点D，由S四边形ABOP=S△AOB+S△AOP，根据三角形的面积公式求解即可；
（3）由S四边形ABOP=S△AOB+S△AOP可得S四边形ABOP=2S△AOB ，即可得到关于m的方程，再解出即可.
试题解析：（1）由
，得a-2=0，b-3=0，c-4=0，∴a=2，b=3，c=4；
（2）
；
（3）存在
，
∴点P的坐标为
.
【题目】（10分）校学生会体育干部想了解七年级学生60秒跳绳的情况，从七年级随机抽取了50名同学的成绩，统计如下：
176 118 94 144 102 92 113 105 108 60
115 104 126 158 105 132 114 118 152 104
151 165 102 132 112 114 118 114 168 172
105 118 68 126 128 139 84 136 76 145
134 128 126 110 96 148 146 156 186 182
（1）以20为组距，补充并完成频数分布表；
（2）请补充未完成的频数直方分布图；
（3）若该校七年级有300名学生，请估计60秒能跳绳120次以上的学生有多少人？
次数分组 | 频数 |
60≤ x < 80 | 3 |
80≤ x < 100 | 4 |
100≤ x < 120 | 19 |
140≤ x < 160 | 8 |
180≤ x < 200 | 2 |
合计 | 50 |
【题目】某蔬菜经营户从蔬菜批发市场批发蔬菜进行零售，部分蔬菜批发价格与零售价格如表：
蔬菜品种 | 西红柿 | 青椒 | 西兰花 | 豆角 |
批发价（元/㎏） | 3.6 | 5.4 | 8 | 4.8 |
零售价（元/㎏） | 5.4 | 8.4 | 14 | 7.6 |
请解答下列问题：
（1）第一天，该经营户批发西红柿和西兰花两种蔬菜共300㎏，用去了1520元钱，这两种蔬菜当天全部售完一共赚了多少元钱？
（2）第二天，该经营户用1520元仍然批发西红柿和西兰花，要想当天全部售完后所赚钱数不少于1050元，则该经营户最多能批发西红柿多少㎏？