题目内容
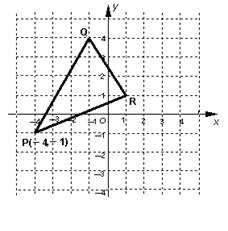
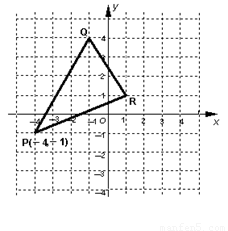
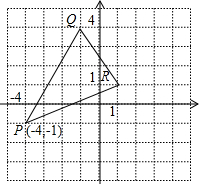 已知△PQR在直角坐标系中的位置如图所示:
已知△PQR在直角坐标系中的位置如图所示:(1)求出△PQR的面积;
(2)画出△P′Q′R′,使△P′Q′R′与△PQR关于y轴对称,写出点P′、Q′、R′的坐标;
(3)连接PP′,QQ′,判断四边形QQ′P′P的形状,求出四边形QQ′P′P的面积.
分析:(1)△PQR的面积从图中可以看出是一个矩形的面积-3个三角形的面积,利用网格就可求出.
(2)从三角形的三个顶点分别向y轴引垂线,并延长,相同长度找到对应点,顺次连接即可.然后从图上读出坐标.
(3)连接,从图上可以看出它是一个等腰梯形,利用梯形的面积公式计算.
(2)从三角形的三个顶点分别向y轴引垂线,并延长,相同长度找到对应点,顺次连接即可.然后从图上读出坐标.
(3)连接,从图上可以看出它是一个等腰梯形,利用梯形的面积公式计算.
解答: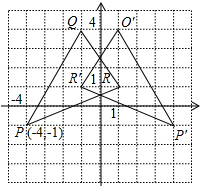 解:(1)S△PQR=5×5-
解:(1)S△PQR=5×5-
×(5×2+3×2+5×3)=9.5;(2分)
(2)△P′Q′R′就是所要画的三角形.
各点坐标分别为P′(4,-1)、Q′(1,4)、
R′(-1,1);(7分)
(3)S=
(2+8)×5=25.(9分)
 解:(1)S△PQR=5×5-
解:(1)S△PQR=5×5-| 1 |
| 2 |
(2)△P′Q′R′就是所要画的三角形.
各点坐标分别为P′(4,-1)、Q′(1,4)、
R′(-1,1);(7分)
(3)S=
| 1 |
| 2 |
点评:本题综合考查了直角坐标系和轴对称图形的性质及梯形的面积公式.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目