题目内容
 已知:在直角坐标系中,直线y=2x+2与x轴交于点A,与y轴交于点B.
已知:在直角坐标系中,直线y=2x+2与x轴交于点A,与y轴交于点B.(1)画出这个函数的图象,并直接写出A,B两点的坐标;
(2)若点C是第二象限内的点,且到x轴的距离为1,到y轴的距离为
| 1 | 2 |
(3)在第(2)题中,作CD⊥x轴于D,那么在x轴上是否存在一点P,使△CDP≌△AOB?若存在,请求出点P的坐标;若不存在,请说明理由.
分析:(1)求出直线上的任意两点,过这两点作直线即可;
(2)若点C是第二象限内的点,且到x轴的距离为1,到y轴的距离为
,可以判断C的坐标是(-
,1),代入直线解析式,即可判断是否在直线上;
(3)可用SAS证明△CDP≌△AOB,即可求得P的坐标.
(2)若点C是第二象限内的点,且到x轴的距离为1,到y轴的距离为
| 1 |
| 2 |
| 1 |
| 2 |
(3)可用SAS证明△CDP≌△AOB,即可求得P的坐标.
解答: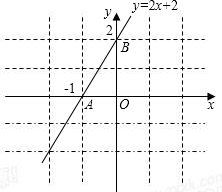 解:(1)如图:A(-1,0),B(0,2)
解:(1)如图:A(-1,0),B(0,2)
(2)可设C点坐标为(m,n)
∵C到x轴的距离为1,到y轴的距离为
∴|m|=
,|n|=1
∴m=±
n=±1(6分)
∵点C是第二象限内的点
∴C点坐标为(-
,1)点
当x=-
时,y=-
×2+2=1,
∴点C在直线y=2x+2上(8分)
(3)存在(9分)
∵|CD|=1,|OA|=1,
∴|CD|=|OA|
又∵点P在x轴上
∴∠CDP=90°=∠AOB
若|DP|=|OB|=2时,可用SAS证明△CDP≌△AOB
∴当P点坐标为(-
+2,0)或(-
-2,0)时
即P点坐标为(1
,0)或(-2
,0)时
△CDP≌△AOB.(14分)
 解:(1)如图:A(-1,0),B(0,2)
解:(1)如图:A(-1,0),B(0,2)(2)可设C点坐标为(m,n)
∵C到x轴的距离为1,到y轴的距离为
| 1 |
| 2 |
∴|m|=
| 1 |
| 2 |
∴m=±
| 1 |
| 2 |
∵点C是第二象限内的点
∴C点坐标为(-
| 1 |
| 2 |
当x=-
| 1 |
| 2 |
| 1 |
| 2 |
∴点C在直线y=2x+2上(8分)
(3)存在(9分)
∵|CD|=1,|OA|=1,
∴|CD|=|OA|
又∵点P在x轴上
∴∠CDP=90°=∠AOB
若|DP|=|OB|=2时,可用SAS证明△CDP≌△AOB
∴当P点坐标为(-
| 1 |
| 2 |
| 1 |
| 2 |
即P点坐标为(1
| 1 |
| 2 |
| 1 |
| 2 |
△CDP≌△AOB.(14分)
点评:本题考查了函数图象的作法,判断一点是否在函数的图象上,以及三角形全等的判定,是数与形结合的比较典型的题目.

练习册系列答案
相关题目
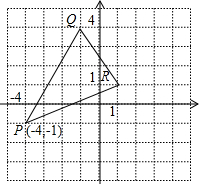 已知△PQR在直角坐标系中的位置如图所示:
已知△PQR在直角坐标系中的位置如图所示: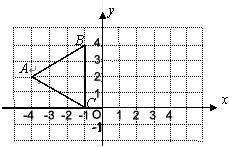 (2006•青岛)已知△ABC在直角坐标系中的位置如图所示,如果△A′B′C′与△ABC关于y轴对称,那么点A的对应点A′的坐标为( )
(2006•青岛)已知△ABC在直角坐标系中的位置如图所示,如果△A′B′C′与△ABC关于y轴对称,那么点A的对应点A′的坐标为( )