Question

如图，将一块斜边长为2的等腰直角三角板（即∠OAB=90°，OB=2，OA=AB）放置在平面直角坐标系的第二象限内，直角边OA落在x轴上．若将三角板绕点O按顺时针方向旋转得到△OA′B′，且OB′恰好也落在x轴上．
（1）求旋转角度的大小；
（2）求直线A′B′对应的函数关系式．

Answer 1

分析：（1）由∠OAB=90°，OB=2，OA=AB，可求得∠AOB的度数，继而求得旋转角度的大小；
（2）首先根据旋转的性质，求得点A′与B′的坐标，然后设直线A′B′对应的函数关系式为y=kx+b，利用待定系数法即可求得答案．

解答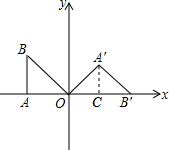：解：（1）∵∠OAB=90°，OA=AB，
∴∠AOB=45°，
∴∠BOB′=180°-∠AOB=135°，
∴旋转角为135°；

（2）过点A′作A′C⊥x轴于点C，
∵∠OAB=90°，OB=2，OA=AB，
∴OB′=OB=2，∠A′OB′=∠AOB=45°，OA′=A′B′，
∴OC=

1

2

OB′=1，
∴A′C=OC=1，
∴A′（1，1），B′（2，0），
设直线A′B′对应的函数关系式为y=kx+b，
∴

1=k+b 0=2k+b

，
解得：

k=-1 b=2

，
∴直线A′B′对应的函数关系式为y=-x+2．

点评：此题考查了旋转的性质、等腰直角三角形的性质以及待定系数法求一次函数解析式．此题难度适中，注意掌握数形结合思想与方程思想的应用．