题目内容
如图，将一块斜边长为12cm，∠B=60°的直角三角板ABC，绕点C沿逆时针方向旋转90°至△A'B'C'的位置，再沿CB向右平移，使点B'刚好落在斜边AB上，那么此三角板向右平移的距离是分析：如图，作B′D∥BC，则B′D即为所求；所以，△AB′D∽△ACB，则
=
，因为AB=12cm，∠B=60°，则可得CB=6cm，根据勾股定理可得AC=6
，又由△A′CB′≌△ACB，可得CB=CB′=6cm，则AB′=6
-6，代入即可求得B′D的长；
| AB′ |
| AC |
| B′D |
| CB |
| 3 |
| 3 |
解答：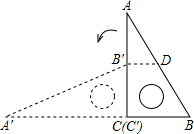
解：如图，作B′D∥BC，则B′D即为所求；
∴△AB′D∽△ACB，则
=
，
∵AB=12cm，∠B=60°，
∴CB=6cm，
∴AC=6
cm，
又∵△A′CB′≌△ACB，
∴CB=CB′=6cm，
∴AB′=（6
-6）cm，
∴
=
，
解得，B′D=（6-2
）cm．
故答案为：（6-2
）．
解：如图，作B′D∥BC，则B′D即为所求；∴△AB′D∽△ACB，则
| AB′ |
| AC |
| B′D |
| CB |
∵AB=12cm，∠B=60°，
∴CB=6cm，
∴AC=6
| 3 |
又∵△A′CB′≌△ACB，
∴CB=CB′=6cm，
∴AB′=（6
| 3 |
∴
6
| ||
6
|
| B′D |
| 6 |
解得，B′D=（6-2
| 3 |
故答案为：（6-2
| 3 |
点评：本题主要考查了平移的性质和旋转的性质，掌握旋转前后的两个三角形全等．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图，将一块斜边长为12cm，∠B=60°的直角三角板ABC，绕点C沿逆时针方向旋转90°至△A′B′C′的位置，再沿CB向右平移，使点B′刚好落在斜边AB上，那么此三角板向右平移的距离是
如图，将一块斜边长为2的等腰直角三角板（即∠OAB=90°，OB=2，OA=AB）放置在平面直角坐标系的第二象限内，直角边OA落在x轴上．若将三角板绕点O按顺时针方向旋转得到△OA′B′，且OB′恰好也落在x轴上．
