Question

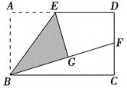
【题目】如图，在矩形ABCD中，，．将矩形ABCD沿过点C的直线折叠，使点B落在对角线AC上的点E处，折痕交AB于点F．

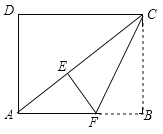
（1）求线段AC的长．

（2）求线段EF的长．

（3）点G在线段CF上，在边CD上存在点H，使以E、F、G、H为顶点的四边形是平行四边形，请画出，并直接写出线段DH的长．

Answer 1

【答案】（1）；（2）；（3）见解析，.

【解析】

（1）根据勾股定理计算AC的长；
（2）设EF=x，在Rt△AEF中，由勾股定理列方程可解答；
（3）先正确画图，根据折叠的性质和平行线的性质证明CH=GH可解答．

解：（1）∵四边形ABCD矩形，.

在中，；

（2）设EF的长为x．

由折叠，得，，，

，，，

在中，，即，

解得．．

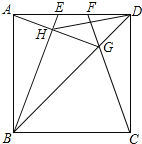
（3）如图，∵四边形EFGH是平行四边形，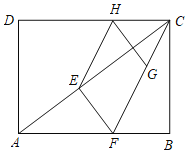

∴EF∥GH，EF=GH=3，
∴∠EFC=∠CGH，
∵AB∥CD，
∴∠BFC=∠DCF，
由折叠得：∠BFC=∠EFC，
∴∠CGH=∠DCF，
∴CH=GH=3，
∴DH=CD-CH=8-3=5．

故答案为：（1）；（2）；（3）见解析，.