题目内容
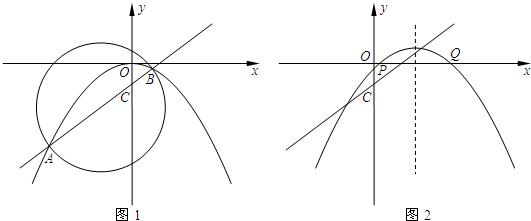
如图1,直线y=| 3 |
| 4 |
| 1 |
| 4 |
(1)求线段AB的长;
(2)若以AB为直径的圆与直线x=m有公共点,求m的取值范围;
(3)如图2,把抛物线向右平移2个单位,再向上平移n个单位(n>0),抛物线与x轴交于P、Q两点,过C、P、Q三点的圆的面积是否存在最小值?若存在,请求出这个最小值和此时n的值;若不存在,请说明理由.
分析:(1)直线解析式与二次函数解析式组成方程组,求得点A,B的坐标,从而求得AB的长.
(2)由点A,B求得圆的圆心设为点O,由AB的长度求得圆半径而得到圆方程,代入x=m求判别式≥0即可.
(3)由抛物线平移后为:y=-
(x-2)2+n,其对称轴是x=2.由于过P、Q的圆的圆心必在对称轴上,要使圆的面积最小,则圆的半径要最小,即点C到圆心的距离要最短,过C作CE垂直抛物线的对称轴,垂足为E,则符合条件的圆是以E为圆心,EC长为半径的圆,求得圆的面积和n的值.
(2)由点A,B求得圆的圆心设为点O,由AB的长度求得圆半径而得到圆方程,代入x=m求判别式≥0即可.
(3)由抛物线平移后为:y=-
| 1 |
| 4 |
解答:解:由题意:
,
解得:x2+3x-4=0,
即x=-4或x=1.
代入求得y=-4或-
,
或
,
即点A(-4,-4)B(1,-
),
则AB=
=
;
(2)由(1)可得A,B中点即圆的圆心点O为(-
,-
),
半径为
AB=
,
∵以AB为直径的圆与x=m②有公共点,
∴-
-
≤m≤-
+
,
即-
≤m≤
;
(3)抛物线平移后为:y=-
(x-2)2+n.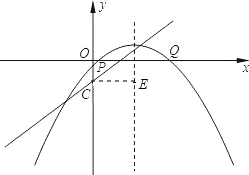
存在.
理由如下:抛物线平移后为:y=-
(x-2)2+n,其对称轴是x=2.
由于过P、Q的圆的圆心必在对称轴上,要使圆的面积最小,则圆的半径要最小,
即点C到圆心的距离要最短,过C作CE垂直抛物线的对称轴,垂足为E,
则符合条件的圆是以E为圆心,EC长为半径的圆,
其面积为4π,n的值0.75.
|
解得:x2+3x-4=0,
即x=-4或x=1.
代入求得y=-4或-
| 1 |
| 4 |
|
|
即点A(-4,-4)B(1,-
| 1 |
| 4 |
则AB=
52+(
|
| 25 |
| 4 |
(2)由(1)可得A,B中点即圆的圆心点O为(-
| 3 |
| 2 |
| 17 |
| 8 |
半径为
| 1 |
| 2 |
| 25 |
| 8 |
∵以AB为直径的圆与x=m②有公共点,
∴-
| 3 |
| 2 |
| 25 |
| 8 |
| 3 |
| 2 |
| 25 |
| 8 |
即-
| 37 |
| 8 |
| 13 |
| 8 |
(3)抛物线平移后为:y=-
| 1 |
| 4 |

存在.
理由如下:抛物线平移后为:y=-
| 1 |
| 4 |
由于过P、Q的圆的圆心必在对称轴上,要使圆的面积最小,则圆的半径要最小,
即点C到圆心的距离要最短,过C作CE垂直抛物线的对称轴,垂足为E,
则符合条件的圆是以E为圆心,EC长为半径的圆,
其面积为4π,n的值0.75.
点评:本题考查了二次方程的综合运用,运用直线和二次函数方程求得交点坐标,以及通过求二次方程的判别式是否≥0,来判定其是否有解.以及考查抛物线的移动问题.

练习册系列答案
相关题目
 如图,一直线与两坐标轴分别交于P(2,0),Q(0,2)两点,A为线段PQ上一点,过点A分别作两坐标轴的垂线,垂足分别为B,C.
如图,一直线与两坐标轴分别交于P(2,0),Q(0,2)两点,A为线段PQ上一点,过点A分别作两坐标轴的垂线,垂足分别为B,C.