题目内容
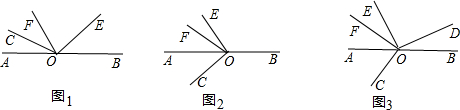
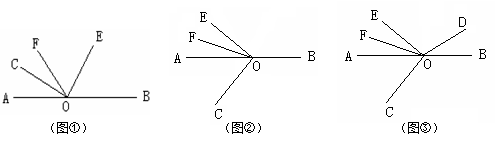
33、已知O为直线AB上的一点,∠COE是直角,OF 平分∠AOE.
(1)如图1,若∠COF=34°,则∠BOE=
(2)当射线OE绕点O逆时针旋转到如图2的位置时,(1)中∠BOE与∠COF的数量关系是否仍然成立?请说明理由.
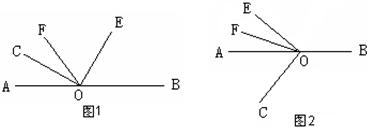
(1)如图1,若∠COF=34°,则∠BOE=
68°
;若∠COF=m°,则∠BOE=2m°
;∠BOE与∠COF的数量关系为∠BOE=2∠COF
.(2)当射线OE绕点O逆时针旋转到如图2的位置时,(1)中∠BOE与∠COF的数量关系是否仍然成立?请说明理由.

分析:(1)由∠COF=34°,∠COE是直角,易求∠EOF,而OE平分∠AOE,可求∠AOE,进而可求∠BOE,若∠COF=m°,则∠BOE=2m°;进而可知∠BOE=2∠COF;
(2)由于∠COE是直角,于是∠EOF=90°-∠COF,而OF平分∠AOE,则有∠AOE=2∠EOF,从而可得∠BOE=180°-∠AOE=180°-2(90°-∠COF)=2∠COF.
(2)由于∠COE是直角,于是∠EOF=90°-∠COF,而OF平分∠AOE,则有∠AOE=2∠EOF,从而可得∠BOE=180°-∠AOE=180°-2(90°-∠COF)=2∠COF.
解答: 解:(1)
解:(1)
∵∠COF=34°,∠COE是直角,
∴∠EOF=90°-34°=56°,
又∵OF平分∠AOE,
∴∠AOE=2∠EOF=112°,
∴∠BOE=180°-112°=68°,
若∠COF=m°,则∠BOE=2m°;
故∠BOE=2∠COF;
故答案是68°;2m°;∠BOE=2∠COF;
(2)∠BOE和∠COF的关系依然成立.
∵∠COE是直角,
∴∠EOF=90°-∠COF,
又∵OF平分∠AOE,
∴∠AOE=2∠EOF,
∴∠BOE=180°-∠AOE=180°-2(90°-∠COF)=2∠COF.
 解:(1)
解:(1)∵∠COF=34°,∠COE是直角,
∴∠EOF=90°-34°=56°,
又∵OF平分∠AOE,
∴∠AOE=2∠EOF=112°,
∴∠BOE=180°-112°=68°,
若∠COF=m°,则∠BOE=2m°;
故∠BOE=2∠COF;
故答案是68°;2m°;∠BOE=2∠COF;
(2)∠BOE和∠COF的关系依然成立.
∵∠COE是直角,
∴∠EOF=90°-∠COF,
又∵OF平分∠AOE,
∴∠AOE=2∠EOF,
∴∠BOE=180°-∠AOE=180°-2(90°-∠COF)=2∠COF.
点评:本题考查了角的计算.解题的关键是注意找出所求角与已知角之间的关系,例如:互余、互补关系.

练习册系列答案
相关题目