题目内容
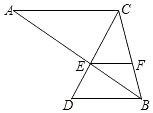
【题目】如图,已知AC∥BD,AB和CD相交于点E,AC=6,BD=4,F是BC上一点,S△BEF:S△EFC=2:3.
(1)求EF的长;
(2)如果△BEF的面积为4,求△ABC的面积.
【答案】(1)![]() ;(2)25.
;(2)25.
【解析】
试题分析:(1)先根据S△BEF:S△EFC=2:3得出CF:BF的值,再由平行线分线段成比例定理即可得出结论;
(2)先根据AC∥BD,EF∥BD得出EF∥AC,故△BEF∽△ABC,再由相似三角形的性质即可得出结论.
试题解析:(1)∵AC∥BD,
∴![]()
∵AC=6,BD=4,
∴![]()
∵△BEF和△CEF同高,且S△BEF:S△CEF=2:3,
∴![]() ,
,
∴![]() .
.
∴EF∥BD,
∴![]() ,
,
∴![]() ,
,
∴![]()
(2)∵AC∥BD,EF∥BD,
∴EF∥AC,
∴△BEF∽△ABC,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∵S△BEF=4,
∴![]() ,
,
∴S△ABC=25.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目



